摘要 建立了變矩器動態運動的廣義方程組和廣義能量方程,并對變矩器一種動態過程進行數值仿真。所建立的廣義方程組對于液力變矩器及傳動鏈中含有變矩器的傳動及控制系統動態研究具有重要意義。
敘詞:變矩器 廣義基本方程組 仿真
中圖分類號:TH137.332
GENERAL EQUATIONS OF TORQUE
CONVERTER AND SIMULATION
CALAULATION
Sun Xuguang Han Decai
(Yanshan University)
Abstract According to the Newton’s law and the conservation the general components equationes and general engery equation of torque converter are given. These are significant for the dynamic processes of torque converter or the control systems which transmision power chain contins torque converter. A kind of dynamic process is also simulated by the numerical method.
Key words:Torque converter Generalized elementary equations Simulation
符 號
角注:1——進口 2——出口 0——穩態 u——u方向 l——液體 p——泵輪 t——渦輪 d——動態m——沿程 j—局部
0 前言
作為一類重要的傳動設備,液力變矩器在傳動領域得到了廣泛應用。此外,它作為一種調控設備來使用也有具體例子[1,2]?。多年來,國內外對變矩器的研究大多數集中在討論及完善其靜態工作理論方面。然而,在傳動和調控應用場合,傳動鏈中包含變矩器的動態工作過程目前尚不能進行合理的分析和仿真計算。由于理論的不足,采用變矩器靜態工作理論來研究和分析變矩器動態工作過程的方法實際已經被采用[3],其方法的不完善是顯然的。因此建立和完善變矩器動態工作過程的分析計算理論是具有實際工程價值和理論意義的,同時它也是一個較新的研究領域。
變矩器是由泵輪、渦輪和導輪組成的復雜液體內循環水力傳動設備。傳統的靜態工作理論是建立在歐拉方程基礎之上,但在動態工作過程中這個基本方程已經不再適用。因此,研究變矩器動態工作理論的一項重要基礎工作就是從最基本的分析入手來提出并且建立合理的基礎方程。
1 變矩器部件液體動態力矩方程
設變矩器內工作液是無粘性的理想流體,對任意瞬時通過變矩器渦輪(圖1)中的微元體dw在z、u、r坐標系中分析,并利用牛頓定律有
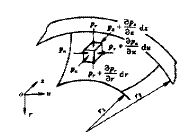
圖1 微元體受力分析
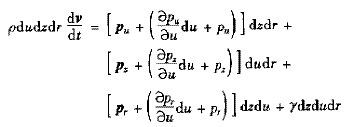
忽略質量力γdzdudr,認為液流是軸對稱和流層間互不干擾,整理并積分上式可得[4]#p#分頁標題#e#
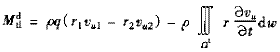 (1)
(1)
注意到泵輪和渦輪是互逆的元件,將上式右邊乘-1有
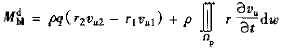 (2)
(2)
由式(1)、(2)可以看到,作用于部件的液體動態力矩是由兩項所決定的。第一項是由瞬時參數q與扭速差Δrv?u乘積所決定,它為對應瞬時參數所表示的穩態力矩項;第二項為動態力矩的附加項,它由圓周分速的微分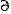 vu/
vu/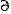 t乘半徑r后的積分所決定,該項可根據葉輪的具體形式得出確定的參數表達式;若忽略該項式子就變成了歐拉方程。此外,對于軸流渦輪的變矩器葉柵有r2=r1=r,因此
t乘半徑r后的積分所決定,該項可根據葉輪的具體形式得出確定的參數表達式;若忽略該項式子就變成了歐拉方程。此外,對于軸流渦輪的變矩器葉柵有r2=r1=r,因此
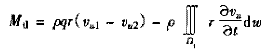 (3)
(3)
上式也就是一些資料中曾提到的水輪機動態力矩的吉諾方程[5]。
2 變矩器部件動態力矩方程
設所研究的變矩器為最常見的三元件向心渦輪變矩器(圖2),由速度三角形有
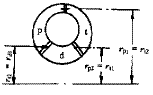
圖2 變矩器結構簡圖
vu=rω+q/A.tanβ
將上式代入式(1)或式(2)的動態附加力矩表達項中有
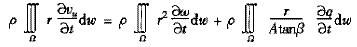
注意到 dω/dt=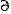 ω/
ω/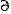 t+
t+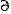 ω/
ω/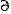 s.ds/dt
s.ds/dt
dq/dt=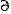 q/
q/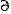 t+
t+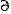 q/
q/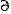 s.ds/dt
s.ds/dt
而 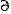 q/
q/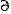 t=
t=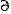 q/
q/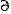 s=0
s=0
整理上式有
對渦輪: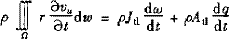
對泵輪: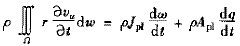
將上面兩個式子及對應穩態力矩項??[6]?分別代入式(1)、(2)有
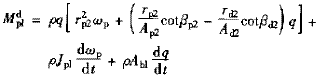 (3)
(3)
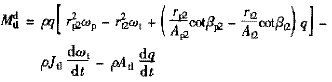 (4)
(4)
式中 Atl,Apl——輪、渦泵輪的面積系數
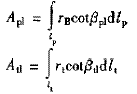
Jpl,Jtl——泵輪、渦輪中工作液體的慣性體積系數
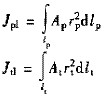
lp,lt——泵輪、渦輪循環圓軸面內中間流線長度
Ap,At——泵輪、渦輪中垂直于中間流線的環型通流面積
對泵輪轉子和渦輪轉子,由力矩平衡關系可得
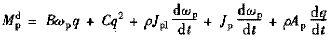 (5)#p#分頁標題#e#
(5)#p#分頁標題#e#
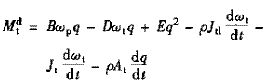 (6)
(6)
式中 Jp,Jt——泵輪、渦輪慣性矩
Mdp,Mdt——泵輪、渦輪外負載動態力矩
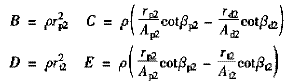
由式(5)、(6)可以看出,泵輪和渦輪作用的外動態力矩等于相應于動態參量所表示的穩態力矩于流量變化及轉速變化所造成的動態附加力矩之和。穩態情況下,式中微分項為零,式子就退化成變矩器部件上作用的穩態力矩表達式。
3 變矩器廣義能量方程
變矩器在動態工作過程中,也要遵守能量守恒原則。根據這條原則可提出變矩器在動態工作過程中其凈輸入能量∑Mdpωp-Mdtωt與其總損失能量γq∑Hcj+∑Hmc之差等于零的能量守恒方程,對常見的三元件變矩器(圖1)可表達如下
Mdpωp-Mdtωt-γq∑Hcj+∑Hmc=0 (7)
式中 泵輪輸入能量
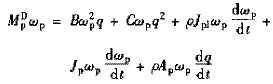
渦輪輸出能量
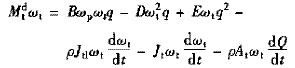
總損失能量
對向心渦輪變矩器,沖擊損失系數一般可取為1,考慮到一般有半徑rp2=rt1,rp1=rt2,rt2=rd1,rp1=rt2,通流面積Ap2=At1,Ap1=At2,At2=Ad1有
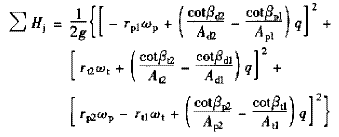
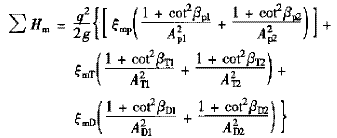
式中 ∑Hj,∑Hm——變矩器總的沖擊和沿程水頭損失
ξm——沿程水頭損失系數
將上面分析式代入能量守恒方程(7)并整理有
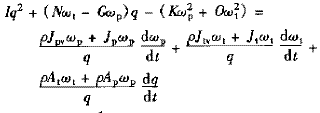 (8)
(8)
式中
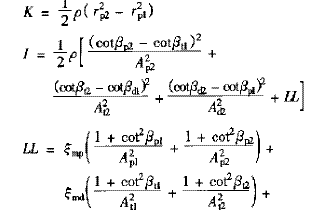
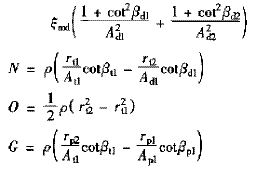
4 變矩器廣義基本方程組及仿真計算
由式(5)、(6)和(8)聯立可得本文提出并且建立的描述變矩器動態運動規律及其動態特性的變矩器廣義方程組。該方程組描述了變矩器動態運動規律下的流量q、力矩Mdp、力矩Mdt、轉速ωt和轉速ωp之間的相互聯系。當方程組式子中的微分項取零,方程組變為常見的變矩器穩態方程組,它說明該廣義方程組既描述動態下變矩器運動規律,也描述了穩態下變矩器運動規律。因此將其稱為液力變矩器廣義方程組,而方程(8)和(5)、(6)分別稱之為變矩器的廣義能量方程和廣義力矩方程。
所得到的廣義方程組是非線性的常微分方程組,要求其解析解是很困難的,但可利用計算數學的方法來求其具有工程價值的數值解。方程組中有5個變量q、Mdp、Mdt、ωt和ωp,因此具體數值求解該方程組尚需根據實際相連的負載和驅動的情況補充另外方程。此外,對該方程組也可作小擾動的線性化分析,并求出它的分析解,該種方法是控制領域常用的求取控制系統模型的理論建模方法。#p#分頁標題#e#
為了方便數值求解和驗證變矩器廣義方程組,這里采用了一種變矩器特殊飛車動態過程(變矩器工作在某穩態工作點,突然將與泵輪及渦輪相連的驅動及負載松開的變矩器動態變化過程),見圖3,對此動態過程有補充方程如下
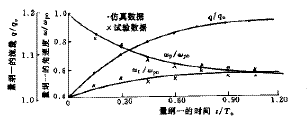
圖3 變矩器飛車動態過程
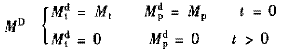
將補充方程代入變矩器廣義方程組可得到3個時間變量的3個常微分方程。該微分方程組可數值求解,方程組中t=0時的穩態參量由穩態方程確定。計算變矩器的參數如下:
cotβp1=-0.280 cotβp1=0
cotβt1=1.121 cotβt2=-1.611
cotβd1=-0.569 cotβd2=2.145
rp1=rt2=rd1=0.059436m
rp2=rt1=rd2=0.059436m
Apl=-0.000331m2
Atl=-0.001090m2
ρJpl+Jp=0.0107608kg.m2
ρJtl+JT=0.0292638kg.m2。
采用四階龍格庫達方法數值求解此動態過程可得圖3,圖中點為試驗結果。可以看出仿真結果與試驗結果吻合較好。
5 結論
由基本定律出發,導出了變矩器廣義力矩方程。由此方程可知,變矩器部件作用的外動態力矩等于相應于動態參量所表示的穩態力矩項于流量變化及轉速變化所造成的動態附加力矩項之和。而傳統的歐拉方程及吉諾方程只是所導出的變矩器部件液體動態力矩的一種特殊情況。
(2)由能量守衡定律出發,提出并建立了變矩器廣義能量方程。
(3)提出并建立了描述變矩器運動的變矩器廣義方程組。該廣義方程組描述了動態下變矩器運動規律,而穩態下變矩器運動規律只是動態下的一種特殊情況。實現了對變矩器動態過程的數值仿真計算,仿真結果符合實際情況。
相關文章
- 2021-09-08BIM技術叢書Revit軟件應用系列Autodesk Revit族詳解 [
- 2021-09-08全國專業技術人員計算機應用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應用 制表、數據處理及宏應用PDF下載
- 2021-08-30從零開始AutoCAD 2014中文版機械制圖基礎培訓教程 [李
- 2021-08-30從零開始AutoCAD 2014中文版建筑制圖基礎培訓教程 [朱
- 2021-08-30電氣CAD實例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風暴2:Maya影像實拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術設計案例教程中文版AutoCAD 建筑設計案例
- 2021-08-29環境藝術制圖AutoCAD [徐幼光 編著] 2013年PDF下載
- 2021-08-29機械AutoCAD 項目教程 第3版 [繆希偉 主編] 2012年PDF