[摘要] 預(yù)應(yīng)力索桿體系在點(diǎn)支式玻璃建筑支承結(jié)構(gòu)中得到了廣泛的應(yīng)用,但對這類體系的原理和特性的認(rèn)識(shí)還很不充分,目前所采用的方法和工具,有些還不能完全反映結(jié)構(gòu)的真實(shí)情況。本文在考慮索桿結(jié)構(gòu)幾何非線性影響的基礎(chǔ)上,利用通用有限元軟件ANSYS 的非線性模塊,對索桿體系初始預(yù)應(yīng)力狀態(tài)和工作狀態(tài)下的結(jié)構(gòu)受力性能進(jìn)行了深入分析。分析結(jié)果表明,利用ANSYS 可以很方便地解決索桿體系的非線性分析問題。
關(guān)鍵詞 索桿結(jié)構(gòu) 非線性原理 有限元分析
1 引言
點(diǎn)支式玻璃幕墻索桿支承體系主要由拉桿(索)式結(jié)構(gòu)組成,即采用不銹鋼拉桿或用與玻璃分縫相對應(yīng)的鋼拉索代替一般的鋼構(gòu)件,形成幕墻的支承結(jié)構(gòu),玻璃通過金屬連接件與其固定。通過給拉桿或拉索施加預(yù)拉應(yīng)力,使其在各種可變荷載作用下都處于受拉狀態(tài),從而達(dá)到用柔性拉桿代替支承結(jié)構(gòu)中的剛性構(gòu)件的目的,避免了構(gòu)件受壓易失穩(wěn)的問題,這樣就可以采用截面較小的高強(qiáng)度鋼構(gòu)件,精致細(xì)巧,大大提高了建筑的通透性。
我國近年來在多項(xiàng)工程中采用了點(diǎn)支式玻璃幕墻技術(shù),如深圳機(jī)場新航站樓、北京遠(yuǎn)洋大廈、北京植物園展覽溫室、南京國際會(huì)展中心和廣州新白云機(jī)場航站樓等多項(xiàng)大型公共工程均采用了點(diǎn)支玻璃幕墻。但該種結(jié)構(gòu)形式在國內(nèi)的研究和應(yīng)用總體上還處于起步階段。
預(yù)應(yīng)力索桿支承體系在點(diǎn)支式玻璃建筑中已經(jīng)得到了大量的、廣泛的應(yīng)用。同工程應(yīng)用相比,理論和試驗(yàn)方面的研究相對滯后。對這類體系的工作原理和結(jié)構(gòu)特性還缺乏充分的認(rèn)識(shí),在實(shí)際工程的分析和計(jì)算中所采用的方法和計(jì)算工具有些還不能完全反映結(jié)構(gòu)的真實(shí)情況。為使索桿支承結(jié)構(gòu)能更加廣泛地在點(diǎn)支式玻璃建筑中的應(yīng)用,需要對其承載性能進(jìn)行深入的研究,同時(shí)對其計(jì)算工具和方法的合理性、有效性進(jìn)行分析論證,從而提出切實(shí)合理且便于工程應(yīng)用的計(jì)算方法。
索桿支承結(jié)構(gòu)依靠自平衡預(yù)應(yīng)力維持結(jié)構(gòu)的穩(wěn)定,在沒有形成預(yù)應(yīng)力之前,結(jié)構(gòu)是處于不穩(wěn)定的機(jī)構(gòu)狀態(tài),這是索桿結(jié)構(gòu)區(qū)別于傳統(tǒng)結(jié)構(gòu)的本質(zhì)特征。在預(yù)應(yīng)力索桿支承結(jié)構(gòu)中,結(jié)構(gòu)剛度貢獻(xiàn)主要來自于初始狀態(tài)預(yù)應(yīng)力。如果不考慮預(yù)應(yīng)力的貢獻(xiàn),初始狀態(tài)的結(jié)構(gòu)剛度往往是奇異的,這就決定了這類結(jié)構(gòu)體系的分析計(jì)算必須采用考慮應(yīng)力剛度矩陣的非線性索桿有限元方法[2]。
索桿支承結(jié)構(gòu)的整體剛度由預(yù)應(yīng)力提供的剛度和截面剛度構(gòu)成。索桿體系設(shè)計(jì)包括初始狀態(tài)設(shè)計(jì)和工作狀態(tài)設(shè)計(jì)兩部分。初始狀態(tài)是指索桿在預(yù)應(yīng)力作用下的自平衡狀態(tài);工作狀態(tài)是指索桿在組合外荷載作用下的平衡狀態(tài)。索桿體系的初始狀態(tài)應(yīng)滿足:初始狀態(tài)是平衡的、穩(wěn)定的,即應(yīng)估算出索(桿)所需的最小張力,以保證工作全過程中索始終處于張緊狀態(tài)。索桿體系的工作狀態(tài)應(yīng)滿足:索桿體系的整體穩(wěn)定、節(jié)點(diǎn)位移應(yīng)滿足要求;索桿體系中的拉索(桿)不宜應(yīng)受壓而退出工作,必須防止應(yīng)拉索(桿)退出工作而使體系成為幾何可變機(jī)構(gòu)。即應(yīng)考慮在對稱和不對稱風(fēng)荷載作用下,能滿足撓度限制和索桿結(jié)構(gòu)強(qiáng)度、穩(wěn)定所需的拉索(桿)中張力。
本文在利用通用有限元分析軟件ANSYS 的非線性模塊,結(jié)合有限元軟件的功能和選用的索單元特點(diǎn),對索桿體系初始預(yù)應(yīng)力狀態(tài)和工作狀態(tài)進(jìn)行了分析。總結(jié)了ANSYS 的有限元分析結(jié)果,研究了索桿體系荷載-位移全過程的結(jié)構(gòu)性能,并對計(jì)算方法進(jìn)行了分析。
2 有限元分析模型
隨著計(jì)算機(jī)技術(shù)、固體力學(xué)和數(shù)值分析科學(xué)的飛速發(fā)展,有限單元法已成為工程數(shù)值分析的強(qiáng)大工具,尤其在固體力學(xué)和結(jié)構(gòu)分析的領(lǐng)域內(nèi),有限元法取得了巨大的進(jìn)展,許多通用程序和專用程序投入實(shí)際應(yīng)用,利用這些程序成功地解決了一大批有重大意義的問題。
非線性問題包括狀態(tài)非線性、材料非線性和幾何非線性等。如果結(jié)構(gòu)承受大變形,它變化的幾何形狀可能會(huì)引起結(jié)構(gòu)的非線性相應(yīng),這就是結(jié)構(gòu)的幾何非線性問題。
索桿支承結(jié)構(gòu)是典型的幾何非線性大變形柔性結(jié)構(gòu)。在該體系中,拉索屬于柔性結(jié)構(gòu),具有大位移、小應(yīng)變的變形特征,雖然構(gòu)件的應(yīng)變?nèi)栽诓牧系膹椥苑秶鷥?nèi),應(yīng)力、應(yīng)交關(guān)系遵從虎克定律,但描述其變形特征的基本關(guān)系-應(yīng)力與位移的關(guān)系是非線性的,其中非線性項(xiàng)的數(shù)值不像小變形問題那樣相對線性項(xiàng)可以略去,而是不可忽略和必須考慮的量。基本關(guān)系的非線性使得所建立的力學(xué)微分方程成為非線性微分方程[4]。#p#分頁標(biāo)題#e#
索桿結(jié)構(gòu)同時(shí)表現(xiàn)出一種與狀態(tài)相關(guān)的非線性行為,例如,一根只能拉伸的鋼索可能是松散的,也可能是繃緊的。相應(yīng)的結(jié)構(gòu)系統(tǒng)的剛度由于系統(tǒng)狀態(tài)的變化而改變,亦即結(jié)構(gòu)的面外剛度可能大大地受結(jié)構(gòu)面內(nèi)應(yīng)力狀態(tài)的影響。這種面內(nèi)應(yīng)力與橫向剛度之間的耦合,通稱為應(yīng)力剛化。在薄的、高應(yīng)力的結(jié)構(gòu)中,如纜索或薄膜中,應(yīng)力剛化現(xiàn)象是相當(dāng)明顯的。
一個(gè)鼓面,當(dāng)它繃緊時(shí)會(huì)產(chǎn)生垂向剛度,這就是應(yīng)力剛化的典型例子。盡管應(yīng)力剛化理論假定單元的轉(zhuǎn)動(dòng)和應(yīng)變是小的,然而在某些結(jié)構(gòu)的系統(tǒng)中,應(yīng)力剛化效應(yīng)只能通過考慮幾何非線性的影響來求得。
在有限元分析中,幾何非線性通常包括初始應(yīng)力效應(yīng),它作為幾何非線性理論的一個(gè)子集,對于大多數(shù)實(shí)體和殼體單元,當(dāng)大變形效應(yīng)被激活時(shí),將自動(dòng)包括初始應(yīng)力剛化效應(yīng)。
為更全面研究索桿結(jié)構(gòu)的承載性能,本文所涉及的幾何非線性分析同時(shí)了考慮應(yīng)力剛化效應(yīng)的影響。
本文選擇目前廣泛采用的索桿支承體系的結(jié)構(gòu)類型,進(jìn)行其初始預(yù)應(yīng)力狀態(tài)和工作狀態(tài)下承載性能的計(jì)算和分析,根據(jù)實(shí)際工程的幾何和荷載參數(shù),建立索桿支承結(jié)構(gòu)的有限元分析模型,進(jìn)行計(jì)算分析。
本文的有限元分析,采用ANSYS 中適用于幾何非線性問題分析的桿單元。在分析中,常用的單元類型為Link8 單元和Link10 單元。Link8 單元只承受軸向力,不承受彎矩和剪力,且具有塑性、蠕變、膨脹、應(yīng)力剛化、大變形、大應(yīng)變、單元死活等功能。在索桿結(jié)構(gòu)分析中,Link8 單元用來模擬其中的剛性桿。
Link10 單元獨(dú)一無二的雙線性剛度矩陣特性,使其成為一個(gè)軸向僅受拉或僅受壓的單元。使用只承受拉力選項(xiàng)時(shí),如果單元受壓,剛度就消失,以此來模擬拉索的松弛。本單元不承受彎矩和剪力,只能軸向承受拉力或壓力。本單元具有應(yīng)力剛化、大變形、大應(yīng)變等功能。在索桿結(jié)構(gòu)分析中,Link10 單元用來模擬其中的拉索(桿)[5]。
由于索桿支承結(jié)構(gòu)工作在彈性階段,因此有限元分析時(shí),可以不考慮結(jié)構(gòu)材料的非線性,僅考慮幾何非線性的影響。有限元分析時(shí),假定材料為各向同性,鋼材的彈性模量E 值按如下采用:普通碳素鋼取2.02×105MPa;不銹鋼和高強(qiáng)碳素鋼為(1.8~2.0)×105MPa,高強(qiáng)鋼絲和鋼絞線取1.5×105MPa,泊松比取0.3。
根據(jù)國家標(biāo)準(zhǔn)《建筑結(jié)構(gòu)荷載規(guī)范》(GB50009-2001)和《點(diǎn)支式玻璃幕墻工程技術(shù)規(guī)程》(CECS:127-2001)的規(guī)定,作用在點(diǎn)支式玻璃幕墻支承結(jié)構(gòu)上的荷載和作用主要有鳳荷載和地震作用。
作用在點(diǎn)支式玻璃幕墻中支承結(jié)構(gòu)的風(fēng)荷載標(biāo)準(zhǔn)值應(yīng)按下式計(jì)算[2.3]:
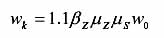
對于豎向的玻璃幕墻,垂直于玻璃平面的分布水平地震作用標(biāo)準(zhǔn)值可按下式計(jì)算[2.3]:
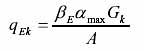
某國際會(huì)展中心點(diǎn)支式玻璃幕墻的豎向?yàn)橹魇芰U件方向,每6.75m 設(shè)有一榀鋼管桁架,承擔(dān)橫向次受力構(gòu)件傳來的水平力。橫向?yàn)榇问芰?gòu)件方向,每1.6m 設(shè)一榀拉桿桁架,承擔(dān)三塊玻璃面板傳來的水平力,拉桿采用不銹鋼棒,規(guī)格為?16,壓桿也為不銹鋼棒,規(guī)格為?40。設(shè)計(jì)簡圖和拉、壓桿件初選截面如圖1 所示。經(jīng)計(jì)算,考慮鳳荷載與地震作用組合下的桁架節(jié)點(diǎn)集中力為:標(biāo)準(zhǔn)值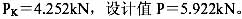
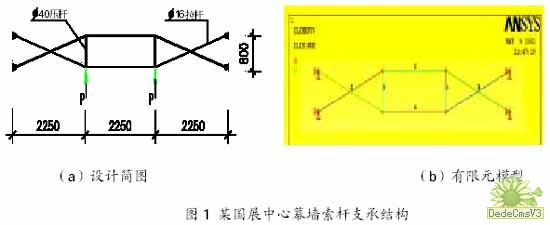
根據(jù)圖1(a)所示的結(jié)構(gòu)設(shè)計(jì)簡圖,利用ANSYS 建立的有限元計(jì)算模型如圖1(b)所示,其中?16 拉桿采用Link10 單元,?40 壓桿采用Link8 單元。
3 幾何非線性分析
首先進(jìn)行索桿支承結(jié)構(gòu)初始預(yù)應(yīng)力分布分析。
假定拉桿預(yù)應(yīng)力初始值,相應(yīng)的初始應(yīng)變?yōu)椋瑢⑵渥鳛樗鲉卧膶?shí)常數(shù)輸入,進(jìn)而得到索桿體系的預(yù)應(yīng)力分布如圖2 所示。
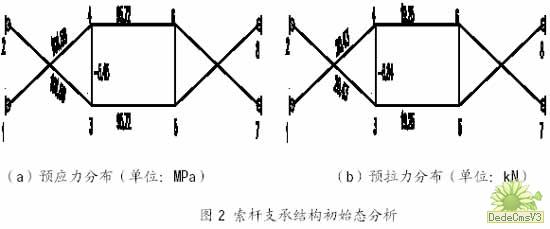
索桿支承結(jié)構(gòu)初始態(tài)預(yù)應(yīng)力分布的分析,是索桿結(jié)構(gòu)承載性能分析的基礎(chǔ)。在初始態(tài)分析階段假定的索桿截面、預(yù)應(yīng)力分布,能否滿足在工作荷載下結(jié)構(gòu)強(qiáng)度、穩(wěn)定和剛度的要求,還有待工作狀態(tài)計(jì)算結(jié)果的驗(yàn)證。#p#分頁標(biāo)題#e#
對具有預(yù)拉力的索桿結(jié)構(gòu)體系在圖1(a)所示水平荷載作用下,進(jìn)行結(jié)構(gòu)的非線性有限元分析。荷載設(shè)計(jì)值作用下的應(yīng)力(內(nèi)力)計(jì)算結(jié)果見圖3 所示。
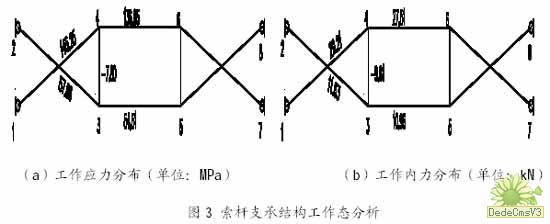
計(jì)算結(jié)果表明,在荷載標(biāo)準(zhǔn)值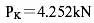 作用下結(jié)點(diǎn)最大位移為1.58mm;在荷載設(shè)計(jì)值
作用下結(jié)點(diǎn)最大位移為1.58mm;在荷載設(shè)計(jì)值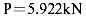 作用下,拉桿最大拉應(yīng)力為145.25MPa,相應(yīng)最大拉力為29.21kN,最小拉力為10.96kN。即結(jié)構(gòu)拉桿的最大、最小拉應(yīng)力及結(jié)構(gòu)的最大位移為:
作用下,拉桿最大拉應(yīng)力為145.25MPa,相應(yīng)最大拉力為29.21kN,最小拉力為10.96kN。即結(jié)構(gòu)拉桿的最大、最小拉應(yīng)力及結(jié)構(gòu)的最大位移為:

以上計(jì)算結(jié)果表明,在工作荷載作用下,索桿結(jié)構(gòu)強(qiáng)度、剛度滿足規(guī)范要求。
4 結(jié)論
計(jì)算結(jié)果表明,采用國際著名通用有限元分析軟件確定預(yù)應(yīng)力索桿體系的初始狀態(tài)和工作狀態(tài),分析計(jì)算方便快捷,計(jì)算結(jié)果準(zhǔn)確可靠,符合工程實(shí)際情況,證明所采用的計(jì)算方法是合理和可行的。
關(guān)鍵詞 索桿結(jié)構(gòu) 非線性原理 有限元分析
1 引言
點(diǎn)支式玻璃幕墻索桿支承體系主要由拉桿(索)式結(jié)構(gòu)組成,即采用不銹鋼拉桿或用與玻璃分縫相對應(yīng)的鋼拉索代替一般的鋼構(gòu)件,形成幕墻的支承結(jié)構(gòu),玻璃通過金屬連接件與其固定。通過給拉桿或拉索施加預(yù)拉應(yīng)力,使其在各種可變荷載作用下都處于受拉狀態(tài),從而達(dá)到用柔性拉桿代替支承結(jié)構(gòu)中的剛性構(gòu)件的目的,避免了構(gòu)件受壓易失穩(wěn)的問題,這樣就可以采用截面較小的高強(qiáng)度鋼構(gòu)件,精致細(xì)巧,大大提高了建筑的通透性。
我國近年來在多項(xiàng)工程中采用了點(diǎn)支式玻璃幕墻技術(shù),如深圳機(jī)場新航站樓、北京遠(yuǎn)洋大廈、北京植物園展覽溫室、南京國際會(huì)展中心和廣州新白云機(jī)場航站樓等多項(xiàng)大型公共工程均采用了點(diǎn)支玻璃幕墻。但該種結(jié)構(gòu)形式在國內(nèi)的研究和應(yīng)用總體上還處于起步階段。
預(yù)應(yīng)力索桿支承體系在點(diǎn)支式玻璃建筑中已經(jīng)得到了大量的、廣泛的應(yīng)用。同工程應(yīng)用相比,理論和試驗(yàn)方面的研究相對滯后。對這類體系的工作原理和結(jié)構(gòu)特性還缺乏充分的認(rèn)識(shí),在實(shí)際工程的分析和計(jì)算中所采用的方法和計(jì)算工具有些還不能完全反映結(jié)構(gòu)的真實(shí)情況。為使索桿支承結(jié)構(gòu)能更加廣泛地在點(diǎn)支式玻璃建筑中的應(yīng)用,需要對其承載性能進(jìn)行深入的研究,同時(shí)對其計(jì)算工具和方法的合理性、有效性進(jìn)行分析論證,從而提出切實(shí)合理且便于工程應(yīng)用的計(jì)算方法。
索桿支承結(jié)構(gòu)依靠自平衡預(yù)應(yīng)力維持結(jié)構(gòu)的穩(wěn)定,在沒有形成預(yù)應(yīng)力之前,結(jié)構(gòu)是處于不穩(wěn)定的機(jī)構(gòu)狀態(tài),這是索桿結(jié)構(gòu)區(qū)別于傳統(tǒng)結(jié)構(gòu)的本質(zhì)特征。在預(yù)應(yīng)力索桿支承結(jié)構(gòu)中,結(jié)構(gòu)剛度貢獻(xiàn)主要來自于初始狀態(tài)預(yù)應(yīng)力。如果不考慮預(yù)應(yīng)力的貢獻(xiàn),初始狀態(tài)的結(jié)構(gòu)剛度往往是奇異的,這就決定了這類結(jié)構(gòu)體系的分析計(jì)算必須采用考慮應(yīng)力剛度矩陣的非線性索桿有限元方法[2]。
索桿支承結(jié)構(gòu)的整體剛度由預(yù)應(yīng)力提供的剛度和截面剛度構(gòu)成。索桿體系設(shè)計(jì)包括初始狀態(tài)設(shè)計(jì)和工作狀態(tài)設(shè)計(jì)兩部分。初始狀態(tài)是指索桿在預(yù)應(yīng)力作用下的自平衡狀態(tài);工作狀態(tài)是指索桿在組合外荷載作用下的平衡狀態(tài)。索桿體系的初始狀態(tài)應(yīng)滿足:初始狀態(tài)是平衡的、穩(wěn)定的,即應(yīng)估算出索(桿)所需的最小張力,以保證工作全過程中索始終處于張緊狀態(tài)。索桿體系的工作狀態(tài)應(yīng)滿足:索桿體系的整體穩(wěn)定、節(jié)點(diǎn)位移應(yīng)滿足要求;索桿體系中的拉索(桿)不宜應(yīng)受壓而退出工作,必須防止應(yīng)拉索(桿)退出工作而使體系成為幾何可變機(jī)構(gòu)。即應(yīng)考慮在對稱和不對稱風(fēng)荷載作用下,能滿足撓度限制和索桿結(jié)構(gòu)強(qiáng)度、穩(wěn)定所需的拉索(桿)中張力。
本文在利用通用有限元分析軟件ANSYS 的非線性模塊,結(jié)合有限元軟件的功能和選用的索單元特點(diǎn),對索桿體系初始預(yù)應(yīng)力狀態(tài)和工作狀態(tài)進(jìn)行了分析。總結(jié)了ANSYS 的有限元分析結(jié)果,研究了索桿體系荷載-位移全過程的結(jié)構(gòu)性能,并對計(jì)算方法進(jìn)行了分析。
2 有限元分析模型
隨著計(jì)算機(jī)技術(shù)、固體力學(xué)和數(shù)值分析科學(xué)的飛速發(fā)展,有限單元法已成為工程數(shù)值分析的強(qiáng)大工具,尤其在固體力學(xué)和結(jié)構(gòu)分析的領(lǐng)域內(nèi),有限元法取得了巨大的進(jìn)展,許多通用程序和專用程序投入實(shí)際應(yīng)用,利用這些程序成功地解決了一大批有重大意義的問題。
非線性問題包括狀態(tài)非線性、材料非線性和幾何非線性等。如果結(jié)構(gòu)承受大變形,它變化的幾何形狀可能會(huì)引起結(jié)構(gòu)的非線性相應(yīng),這就是結(jié)構(gòu)的幾何非線性問題。
索桿支承結(jié)構(gòu)是典型的幾何非線性大變形柔性結(jié)構(gòu)。在該體系中,拉索屬于柔性結(jié)構(gòu),具有大位移、小應(yīng)變的變形特征,雖然構(gòu)件的應(yīng)變?nèi)栽诓牧系膹椥苑秶鷥?nèi),應(yīng)力、應(yīng)交關(guān)系遵從虎克定律,但描述其變形特征的基本關(guān)系-應(yīng)力與位移的關(guān)系是非線性的,其中非線性項(xiàng)的數(shù)值不像小變形問題那樣相對線性項(xiàng)可以略去,而是不可忽略和必須考慮的量。基本關(guān)系的非線性使得所建立的力學(xué)微分方程成為非線性微分方程[4]。#p#分頁標(biāo)題#e#
索桿結(jié)構(gòu)同時(shí)表現(xiàn)出一種與狀態(tài)相關(guān)的非線性行為,例如,一根只能拉伸的鋼索可能是松散的,也可能是繃緊的。相應(yīng)的結(jié)構(gòu)系統(tǒng)的剛度由于系統(tǒng)狀態(tài)的變化而改變,亦即結(jié)構(gòu)的面外剛度可能大大地受結(jié)構(gòu)面內(nèi)應(yīng)力狀態(tài)的影響。這種面內(nèi)應(yīng)力與橫向剛度之間的耦合,通稱為應(yīng)力剛化。在薄的、高應(yīng)力的結(jié)構(gòu)中,如纜索或薄膜中,應(yīng)力剛化現(xiàn)象是相當(dāng)明顯的。
一個(gè)鼓面,當(dāng)它繃緊時(shí)會(huì)產(chǎn)生垂向剛度,這就是應(yīng)力剛化的典型例子。盡管應(yīng)力剛化理論假定單元的轉(zhuǎn)動(dòng)和應(yīng)變是小的,然而在某些結(jié)構(gòu)的系統(tǒng)中,應(yīng)力剛化效應(yīng)只能通過考慮幾何非線性的影響來求得。
在有限元分析中,幾何非線性通常包括初始應(yīng)力效應(yīng),它作為幾何非線性理論的一個(gè)子集,對于大多數(shù)實(shí)體和殼體單元,當(dāng)大變形效應(yīng)被激活時(shí),將自動(dòng)包括初始應(yīng)力剛化效應(yīng)。
為更全面研究索桿結(jié)構(gòu)的承載性能,本文所涉及的幾何非線性分析同時(shí)了考慮應(yīng)力剛化效應(yīng)的影響。
本文選擇目前廣泛采用的索桿支承體系的結(jié)構(gòu)類型,進(jìn)行其初始預(yù)應(yīng)力狀態(tài)和工作狀態(tài)下承載性能的計(jì)算和分析,根據(jù)實(shí)際工程的幾何和荷載參數(shù),建立索桿支承結(jié)構(gòu)的有限元分析模型,進(jìn)行計(jì)算分析。
本文的有限元分析,采用ANSYS 中適用于幾何非線性問題分析的桿單元。在分析中,常用的單元類型為Link8 單元和Link10 單元。Link8 單元只承受軸向力,不承受彎矩和剪力,且具有塑性、蠕變、膨脹、應(yīng)力剛化、大變形、大應(yīng)變、單元死活等功能。在索桿結(jié)構(gòu)分析中,Link8 單元用來模擬其中的剛性桿。
Link10 單元獨(dú)一無二的雙線性剛度矩陣特性,使其成為一個(gè)軸向僅受拉或僅受壓的單元。使用只承受拉力選項(xiàng)時(shí),如果單元受壓,剛度就消失,以此來模擬拉索的松弛。本單元不承受彎矩和剪力,只能軸向承受拉力或壓力。本單元具有應(yīng)力剛化、大變形、大應(yīng)變等功能。在索桿結(jié)構(gòu)分析中,Link10 單元用來模擬其中的拉索(桿)[5]。
由于索桿支承結(jié)構(gòu)工作在彈性階段,因此有限元分析時(shí),可以不考慮結(jié)構(gòu)材料的非線性,僅考慮幾何非線性的影響。有限元分析時(shí),假定材料為各向同性,鋼材的彈性模量E 值按如下采用:普通碳素鋼取2.02×105MPa;不銹鋼和高強(qiáng)碳素鋼為(1.8~2.0)×105MPa,高強(qiáng)鋼絲和鋼絞線取1.5×105MPa,泊松比取0.3。
根據(jù)國家標(biāo)準(zhǔn)《建筑結(jié)構(gòu)荷載規(guī)范》(GB50009-2001)和《點(diǎn)支式玻璃幕墻工程技術(shù)規(guī)程》(CECS:127-2001)的規(guī)定,作用在點(diǎn)支式玻璃幕墻支承結(jié)構(gòu)上的荷載和作用主要有鳳荷載和地震作用。
作用在點(diǎn)支式玻璃幕墻中支承結(jié)構(gòu)的風(fēng)荷載標(biāo)準(zhǔn)值應(yīng)按下式計(jì)算[2.3]:
對于豎向的玻璃幕墻,垂直于玻璃平面的分布水平地震作用標(biāo)準(zhǔn)值可按下式計(jì)算[2.3]:
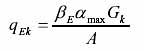
某國際會(huì)展中心點(diǎn)支式玻璃幕墻的豎向?yàn)橹魇芰U件方向,每6.75m 設(shè)有一榀鋼管桁架,承擔(dān)橫向次受力構(gòu)件傳來的水平力。橫向?yàn)榇问芰?gòu)件方向,每1.6m 設(shè)一榀拉桿桁架,承擔(dān)三塊玻璃面板傳來的水平力,拉桿采用不銹鋼棒,規(guī)格為?16,壓桿也為不銹鋼棒,規(guī)格為?40。設(shè)計(jì)簡圖和拉、壓桿件初選截面如圖1 所示。經(jīng)計(jì)算,考慮鳳荷載與地震作用組合下的桁架節(jié)點(diǎn)集中力為:標(biāo)準(zhǔn)值

根據(jù)圖1(a)所示的結(jié)構(gòu)設(shè)計(jì)簡圖,利用ANSYS 建立的有限元計(jì)算模型如圖1(b)所示,其中?16 拉桿采用Link10 單元,?40 壓桿采用Link8 單元。
3 幾何非線性分析
首先進(jìn)行索桿支承結(jié)構(gòu)初始預(yù)應(yīng)力分布分析。
假定拉桿預(yù)應(yīng)力初始值,相應(yīng)的初始應(yīng)變?yōu)椋瑢⑵渥鳛樗鲉卧膶?shí)常數(shù)輸入,進(jìn)而得到索桿體系的預(yù)應(yīng)力分布如圖2 所示。

索桿支承結(jié)構(gòu)初始態(tài)預(yù)應(yīng)力分布的分析,是索桿結(jié)構(gòu)承載性能分析的基礎(chǔ)。在初始態(tài)分析階段假定的索桿截面、預(yù)應(yīng)力分布,能否滿足在工作荷載下結(jié)構(gòu)強(qiáng)度、穩(wěn)定和剛度的要求,還有待工作狀態(tài)計(jì)算結(jié)果的驗(yàn)證。#p#分頁標(biāo)題#e#
對具有預(yù)拉力的索桿結(jié)構(gòu)體系在圖1(a)所示水平荷載作用下,進(jìn)行結(jié)構(gòu)的非線性有限元分析。荷載設(shè)計(jì)值作用下的應(yīng)力(內(nèi)力)計(jì)算結(jié)果見圖3 所示。

計(jì)算結(jié)果表明,在荷載標(biāo)準(zhǔn)值

以上計(jì)算結(jié)果表明,在工作荷載作用下,索桿結(jié)構(gòu)強(qiáng)度、剛度滿足規(guī)范要求。
4 結(jié)論
計(jì)算結(jié)果表明,采用國際著名通用有限元分析軟件確定預(yù)應(yīng)力索桿體系的初始狀態(tài)和工作狀態(tài),分析計(jì)算方便快捷,計(jì)算結(jié)果準(zhǔn)確可靠,符合工程實(shí)際情況,證明所采用的計(jì)算方法是合理和可行的。
相關(guān)文章
- 2021-09-08全國專業(yè)技術(shù)人員計(jì)算機(jī)應(yīng)用能力考試用書 AutoCAD2004
- 2021-08-28計(jì)算機(jī)輔助設(shè)計(jì)與制造 21世紀(jì)全國應(yīng)用型本科大機(jī)械系
- 2021-08-28計(jì)算機(jī)輔助設(shè)計(jì)與制造(CAD∕CAM)PDF下載
- 2021-08-27計(jì)算機(jī)輔助設(shè)計(jì)與制造 21世紀(jì)全國應(yīng)用型本科大機(jī)械系
- 2021-08-27計(jì)算機(jī)輔助設(shè)計(jì)與制造(CAD∕CAM)PDF下載
- 2021-08-14新編AutoCAD 2004中文版計(jì)算機(jī)輔助設(shè)計(jì)應(yīng)用技能培訓(xùn)教
- 2021-08-13中文AutoCAD 2008計(jì)算機(jī)輔助設(shè)計(jì)實(shí)訓(xùn)教程PDF下載
- 2021-08-03Autodesk RevitStructure2012應(yīng)用寶典 [歐特克軟件(中
- 2021-08-02Autodesk RevitMEP2012應(yīng)用寶典 [歐特克軟件(中國)有限
- 2021-08-02Autodesk Revit2013族達(dá)人速成 [歐特克軟件(中國)有限公