公差設計與制造成本
時間:2011-04-20 08:17:03 來源:未知
1 簡介
公差設計應在使用要求及加工能力的約束下以成本最低作為目標函數。此成本應是包含了產品生命期中多項成本因素的綜合的總成本,其中包括制造成本、質量損失成本、廢次品損失成本、庫存成本及機會損失成本等。制造成本是指產品在制造過程中發生的各種損耗的總和,是各種成本因素中最直接、最必不可少的成本因素。因此,對公差與制造成本進行建模是公差優化中的基礎問題。
在很多情況下,設計師手中并未掌握有效的成本信息,其設計公差僅僅是從滿足使用要求的角度來考慮的。任何設計均要通過制造過程來實現,在該過程中必然要造成成本損耗,而成本的多寡作為反饋信息將促使設計師調整其設計方案。通過多次實踐調整最終達到以成本最低為目標的最優設計方案。顯然,這種優化過程必然是以大量的成本浪費作為代價的。解決此問題的關鍵應在于使設計師掌握制造過程中的成本信息,使其在設計的同時就能進行基于成本的優化。對公差與制造成本的關系進行建模,即是為設計師提供此優化的依據。
虛擬制造要求對整個制造系統進行建模,使設計師在得出某一設計方案的同時就能擬合出實現該方案的整個制造過程,從而對設計方案進行評價和修改。并行工程要求在進行產品設計的同時,就要考慮其制造加工過程的可行性與成本問題。因此,對公差與制造成本關系進行建模,是符合先進制造的整體思想的,該模型也將成為虛擬制造與并行工程中的基礎模型之一。
對設計公差與成本關系的建模方法應根據設計師所掌握的制造系統信息的不同而有所不同。在很多情況下,公差設計師不能獲取制造系統的詳細資料,不能確定設計公差所對應的工藝方法以及制造過程中的各種損耗,因此不能直接計算設計公差所對應的制造成本。但設計師能夠獲得一組經驗公差—成本數據,即某些公差值所對應的成本數據。這些公差值是間斷的,而設計師往往需要掌握各種精度范圍內的公差—成本數據。也就是說,設計師需要掌握一條連續、完整的公差—成本關系曲線,而我們所已知的只是曲線上的一些離散點。此時即可利用曲線擬合法進行建模,在這些已知數據點的基礎上擬合出一條完整的公差—成本曲線,從而為設計師提供任意精度范圍內的公差—成本關系。
曲線擬合法即是將已有的公差—成本數據作依據,以某一曲線來對上述數據進行擬合,從而得到連續的公差—成本關系曲線,并以此作為今后設計的依據。應該指出,曲線擬合法是以某些公差—成本數據來推知其它公差所對應的成本,因此其基本假設是所有公差所對應的成本均是在同一制造系統中產生的,即制造系統的狀態未發生改變。如制造系統狀態發生了改變,根據已知的數據點是無法推測其它公差所對應的成本的。此時使用曲線擬合法必然帶來較大的系統誤差。
在此研究領域,Speckhart提出了指數模型,Spotts提出了倒數平方模型,Dong & Hu提出了多項式模型,S.H.Yeo等提出了自然樣條模型。本文對以上傳統的曲線擬合法進行了深入的研究對比,對公差—成本曲線進行了較詳細的分析,在此基礎上,提出了對公差—成本曲線進行分段擬合的建模方法。
2 公差—成本曲線
設計公差在制造系統中的實現總是通過一定的工藝序列完成的,如加工?80h7軸的工藝序列為粗車—半精車—精車。一定的工藝序列有其一定的加工能力范圍,當公差變化到一定程序時會引起工藝序列的變化,如粗車—半精車—粗磨—精磨。實驗證明,同一工藝序列的公差—成本曲線與工藝序列變化時的曲線有不同的特征。
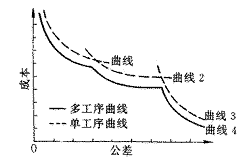
圖1 公差成本曲線
考慮圖1所示的公差—成本曲線,其中δ為公差,c為成本,可看作是公差的函數,記為c(δ)。同一工藝序列公差—成本曲線的特征可歸納如下:
#p#分頁標題#e#
- 曲線位于第一象限,且單調遞減(不嚴格)
- 當δ→0時,c →+∞且c′(δ)→-∞
- 當δ→+∞時,c →B0(常數)且c′(δ)→0
- 曲線呈現凸函數曲線特征,無拐點
工藝序列變化時的公差—成本曲線是由多條同一工藝序列的曲線按照成本最低原則組合而成,其局部特點保留了同一工藝序列曲線的特征,曲線具有明顯的分段性。
在設計師獲取的經驗數據中,特別是公差跨度范圍較大的數據中,不同公差的實現往往采用了不同的工藝方法,因此我們擬合的對象應是工藝序列變化時的公差—成本曲線。
3 公差—成本曲線的分段擬合法
為了對經驗成本—公差數據進行曲線擬合,Speckhart提出了指數模型,Spotts提出了倒數平方模型,Dong & Hu提出了多項式模型,S.H.Yeo等提出了自然樣條模型。其中指數模型及倒數平方模型以及其它類似模型對數據點進行整體擬合,其曲線符合同一工藝序列公差—成本曲線的特征,即“合理”,但當數據組中包含工藝序列的變化時,在曲線中段的擬合精度不理想。多項式模型力圖使擬合曲線在數據點上做到完全精確,但由于其振動問題(龍格現象),使整體曲線不符合公差—成本曲線的基本特征,出現遞增段,甚至出現成本負值,即曲線不合理。自然樣條法假設相鄰數據點間的曲線為三次多項式,且要求整個曲線的一階、二階導數連續,以至于出現與多項式模型同樣的問題。因此,曲線擬合法的關鍵在于對數據點進行正確的分段,并在各段采用符合單工序曲線特征的函數來進行擬合。
對多工序公差—成本曲線進行擬合的首要問題在于對數據點的正確分段。利用單工序曲線的凸函數特征,本文提出了斜率判斷法:設ki為數據點(xi,yi)與(xi+1,yi+1)間連線的斜率,應有ki≤0。如|ki|<|ki+1|,則在xi與xi+1之間,曲線分段。
對分段后的曲線,可分別采用具有單工序曲線特征的函數進行擬合。考慮到指數模型能夠合理地體現單工序曲線的特征,并且運用較為成熟,本文選用指數模型對各段曲線進行擬合。模型表達式為
公差
1
2
4
8
16
30
60
120
成本
3.513
2.48
1.24
1.24
1.20
0.413
0.413
0.372
現舉實例說明分段法的運用。下表為一組已知公差—成本數據。
分別計算相鄰數據點連線的斜率為:-1.033、-0.62、0、-0.005、-0.056、0、0。根據斜率判斷法,在數據點(8,1.24)與(16,1.20)之間進行分段。用指數模型進行擬合后,表達式與曲線如圖2所示。
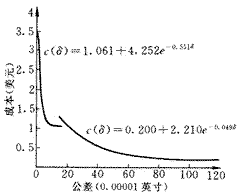
圖2 多工序公差—成本曲線的分段擬合
分段曲線擬合法所得出的公差—成本曲線體現了產品加工的多工藝序列手段。曲線的分段體現了工藝序列的改變。在同一工藝序列,即同一段曲線上,制造成本隨公差要求的提高而增加。每一工藝序列都具有一定的加工能力范圍,即當公差要求增加到某一值,成本趨于無窮大。每一工藝序列都具有基本成本,公差要求降低到一定程序,成本不再降低,即曲線趨于水平。工藝序列變化的曲線是由多條同一工藝序列曲線以成本最低為原則組合而成的。值得注意的是,工藝序列變化曲線中的各段曲線可拓展成多條獨立的同一工藝序列曲線,當系統出現特殊狀態,如某一工序發生故障,即可尋找其他替代工藝序列,而這種替代將是以成本增加作為代價的。
#p#分頁標題#e#工藝序列變化的公差—成本曲線不僅體現了成本隨公差變化的整體趨勢,同時也可反映出制造系統的加工水平。某國營中型企業近期進行了設備技術改造。原來主要加工方法為車削,主要加工工序為粗車—半精車—精車,隨著零件使用要求的逐步提高,公差要求逐漸嚴格,精車工序須采用復雜精密卡具及高技術,有經驗的工人才能達到要求,制造成本明顯提高,而磨削工序由于機床數量少并且型號老化,開機成本較高,因此較少使用。經過設備技術改造,引進了一批新型磨床,并進行了人員培訓同時制定了有效的管理方法,大大降低了磨削工序的使用成本。改進后工廠的主要工序轉為粗車—半精車—粗磨—半精磨,大幅度提高了加工能力及質量。通過對該廠改造前后的公差—制造成本數據進行擬合,得出曲線如圖3所示。可從以下幾個方面對該圖進行分析:
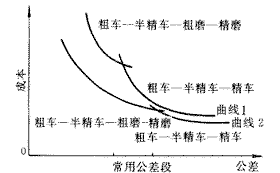
圖3 制造系統改進前后的公差成本曲線
- .在常用公差段內,曲線2在曲線1的下方,即實現相同公差值,改造后的制造系統所耗費的成本較少,從而體現了改造后系統的生產及管理水平高于改造前。
- 曲線2在曲線1的左方,即改造后系統的加工能力范圍大于改造前系統,體現了系統技術水平的提高。
- 曲線2中磨削加工與車削加工的交點比曲線1靠右,表明改造后系統更加大范圍地使用較高水平的加工方法,即高水平的加工方法更加成熟。
通過對公差—制造成本曲線的分析可得出,改造后制造系統的整體水平優于改造前。
4 結論
運用曲線擬合法進行優化設計,可避免由實際制造的成本過高而修改設計造成的損失,同時也大大縮短了設計周期,提高了設計的靈敏度。采用曲線擬合法得出的公差—制造成本曲線,還反映了制造系統的整體信息,對公差—制造成本曲線進行分析和比較,可對制造系統的加工能力及管理水平進行評價。因此,運用曲線擬合法對公差與制造成本的關系進行建模,符合先進制造的整體思想,是公差優化中的基礎理論依據。


