CNC系統(tǒng)中任意空間曲線的插補(bǔ)方法
時(shí)間:2011-05-20 08:43:10 來(lái)源:未知
在CNC機(jī)床上加工工件,無(wú)論是加工曲面還是曲線,加工過(guò)程的刀具中心軌跡都是曲線。傳統(tǒng)的CNC機(jī)床只能加工簡(jiǎn)單的直線和圓弧等曲線,加工復(fù)雜的曲線需要在編程時(shí)轉(zhuǎn)化為簡(jiǎn)單曲線。隨著計(jì)算機(jī)技術(shù)的發(fā)展和機(jī)械零件復(fù)雜程度的提高,人們希望CNC機(jī)床能直接加工任意空間曲線。尤其樣條曲線的發(fā)展,這種希望更迫切。本文運(yùn)用數(shù)據(jù)采樣時(shí)間分割法和泰勒(Taylor)公式,推導(dǎo)出一種任意參數(shù)曲線的等速進(jìn)給實(shí)時(shí)插補(bǔ)算法。下面給以介紹。
1 參數(shù)曲線插補(bǔ)算法
一般曲線c可寫成如下形式
c(u)={x(u),y(u),z(u)} uÎ[u0,un]
(1)
u是任意參數(shù),通常0≤u≤1。大多數(shù)CAD/CAM系統(tǒng)采用參數(shù)形式表示曲線。用參數(shù)描述曲線有以下優(yōu)點(diǎn):參數(shù)形式曲線對(duì)于控制多軸機(jī)床是非常方便的,每個(gè)軸可以單獨(dú)驅(qū)動(dòng)。另外,曲線上點(diǎn)的計(jì)算容易,這是由于x,y,z都是參數(shù)u的顯函數(shù),故易于計(jì)算。
CNC系統(tǒng)插補(bǔ)器的任務(wù)是在恒插補(bǔ)周期T(T是常數(shù),一般為1~10ms)內(nèi)計(jì)算輸出一次由下式確定的進(jìn)給弦長(zhǎng)DL(uk)在x,y,z軸上的坐標(biāo)分量
DL(uk={x(uk+1)-x(uk),y(uk+1)-y(uk),z(uk+1)-z(uk)}
k=1,2,…,n-1
(2)
CNC系統(tǒng)要求每次插補(bǔ)所形成的弦長(zhǎng)相等,因此,實(shí)時(shí)插補(bǔ)方法不能建立在參數(shù)的等分上,而應(yīng)建立在每個(gè)進(jìn)給步長(zhǎng)DLk相等的基礎(chǔ)上。現(xiàn)在的關(guān)鍵是推導(dǎo)出弦長(zhǎng)相等的條件下相應(yīng)的參數(shù)增量Duk。以下是恒速進(jìn)給實(shí)時(shí)插補(bǔ)算法的具體推導(dǎo)。
沿參數(shù)曲線的進(jìn)給速度可按下式計(jì)算
V(u)=
ds
=(
ds
)(
du
)
dt
du
dt
(3)
(4)
其中s為曲線的自然參數(shù)即弧長(zhǎng),有
ds
=[(x')2+(y')2+(z')2]½
dt
(5)
x'=
dx
y'=
dy
z'=
dz
du
du
du
式(4)要求ds/du≠0,由式(5)知,即要求該曲線為正則曲線。
把式(5)代入式(4),得
花少量的時(shí)間計(jì)算式(6)的解是實(shí)時(shí)插補(bǔ)算法的關(guān)鍵,然而V為常值條件下的解u(t)一般難以求得。因此,不妨在t=kT處使用泰勒(Taylor)級(jí)數(shù)展開(kāi)進(jìn)行迭代求解。由泰勒公式得
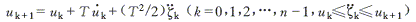 (7)
(7)
最后一項(xiàng)為一階泰勒公式的余項(xiàng),是二階無(wú)窮小量,對(duì)于插補(bǔ)計(jì)算可忽略不計(jì)。把式(6 )代入式( 7 ) ,忽略二階余項(xiàng),得
uk+1=uk+
VT
(x'2+y'2+z'2)½
(8)
由式(8 )確定uk+1代入式(1 )和式(2 )即可計(jì)算出插補(bǔ)步長(zhǎng)DL((u )k)的各個(gè)坐標(biāo)分量。該算法的優(yōu)點(diǎn)就是保證插補(bǔ)點(diǎn)始終在曲線上,無(wú)累積誤差,只有弓高誤差。
2 最大插補(bǔ)步長(zhǎng)和弓高誤差的關(guān)系
由以上恒速實(shí)時(shí)插補(bǔ)算法推導(dǎo)可知,插補(bǔ)點(diǎn)始終在曲線上,無(wú)累積誤差,因此弓高誤差就是插補(bǔ)誤差。弓高誤差d受給定精度指標(biāo)e的限制,即必須有d≤e。實(shí)際加工的弓高誤差取決于插補(bǔ)步長(zhǎng)DLk 、曲線的曲率k和撓率t。k和t由下式?jīng)Q定。
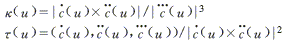 (9)
(9)
(10)
由于插補(bǔ)步長(zhǎng)很短,因此可將被插補(bǔ)弧看作半徑為Rk的圓弧。這樣的簡(jiǎn)化是偏安全的。Rk由下式?jīng)Q定
Rk=1/max(k(ui),t(ui)) (k,i=0,1,2,…n-1;uk≤ui≤uk+1
(11)
那么,DLk逼近曲線弧DCk的弓高誤差dk如圖1所圖。圖1中,DLk和dk之間的關(guān)系可表達(dá)為
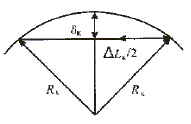
圖1 弓高與步長(zhǎng)的關(guān)系
若對(duì)任意t∈[0,1] ,要求插補(bǔ)器輸出由式(2 )給定的 DLk逼近對(duì)應(yīng)的曲線弧DCk時(shí),弓高誤差對(duì)所有k均有#p#分頁(yè)標(biāo)題#e#dk≤e,則最大插補(bǔ)步長(zhǎng)可表示為
式(13 )中R由下式?jīng)Q定
R=1/max[max(k(u)),max(t(u))] u∈[u0,un]
(14)
式(14 )可由參數(shù)方程(1)代入式(9 )、式(10 ) ,分別用普通函數(shù)求最大值的方法得到。
3 結(jié)束語(yǔ)
本文介紹的插補(bǔ)方法能用在所有以參數(shù)方程表示的任意空間曲線上。這些曲線可包括B樣條等所有樣條曲線。計(jì)算的復(fù)雜程度也不是很高,一般帶浮點(diǎn)運(yùn)算器的計(jì)算機(jī)都能勝任,加之插補(bǔ)時(shí)間固定,能很好地滿足控制系統(tǒng)對(duì)實(shí)時(shí)性的要求。
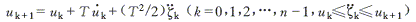 (7)
(7)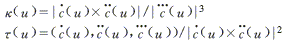 (9)
(9)