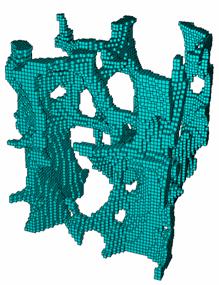
| 人類骨小梁的非線性細觀有限元分析 | |||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
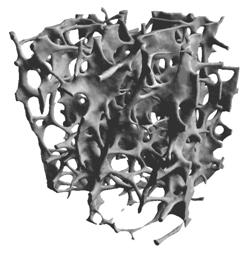
摘要骨小梁必須能夠承受日常行為和受傷時引起的載荷。由于骨小梁的高度多孔性和復雜結構,并且這種多孔性和復雜結構在不同的解剖部位和不同的個人之間,差異極大,因而研究骨小梁的機械特性非常具有挑戰性。雖然細觀有限元分析 (μFE) 是分析骨小梁機械特性的最常用的方法,但由于這些模型的尺寸很大,迫使研究人員使用自定義代碼和線性分析方法。Abaqus 的非線性功能可以對這些模型進行有效分析,為重要的研究課題提供答案。 Abaqus 的主要功能和優點建立模擬骨骼組織機械特性的本構模型 |
|||||||||||||||||||||||||||||||||||||||
模型 |
單元數量 |
節點數 |
自由度數 |
|
圓柱體 |
828,853 |
1,380,834 |
4,142,502 |
|
立方體 |
131,322 |
216,027 |
648,081 |
圓柱體模型被用來評定直接稀疏求解器的并行處理能力。在沒有摩擦的情況下,在頂面和底面應用位移邊界條件,模擬 1% 壓縮應變。分別用 HP rx8620 計算機中 1、2和4 個 CPU 進行線彈性分析。
利用邊長為 5 毫米的立方體模型進行非線性分析。這個尺寸的立方體已大得足夠確定平面特性,同時又小得足夠確保非線性分析的可行性。骨骼組織模型是用鑄鐵塑性材料制造的。鑄鐵塑性材料在受到拉伸和壓縮時,其彈塑性狀態會有不同的屈服強度和硬化,因此會產生一個非對稱的單元剛度矩陣。因此,需要使用非對稱存儲的并行稀疏直接求解器。樣本是一個彈性模量為 13.4Gpa,泊松比為 0.3 的組織。(參見參考文獻 2)根據人類股骨骨小梁組織的屈服應變(參見參考文獻 3),鑄鐵塑性模型組織拉伸時的屈服應力為 55.2MPa,壓縮時為 110.6MPa。在拉伸和壓縮時,使用的是相當于彈性模量 5% 的硬化斜度。在無摩擦的位移邊界條件下,拉伸和壓縮采用了 2% 的公稱應變。在這樣低的公稱應變條件下,骨骼微結構的自力接觸可以忽略。此外,每個模型都進行了考慮和不考慮幾何非線性變形的模擬。總共進行了四個非線性分析,為了進行比較,還計算了平面屈服應變。所有對立方體的分析都是在一臺 IBM Power4 計算機上進行的,使用了兩個 CPU。
結果和結論
利用 4 個 CPU 對圓柱體模型進行線性分析,用時不到 16 分鐘,占用內存不到 11 GB(參見表 2)。表 2 還包括了平行直接求解器的計數結果;加速因數是根據求解時間得到的。對具有幾何非線性的立方體 μFE 模型進行非線性分析,用時不到 7.4 小時,占用內存 4.1 GB。每個非線性分析需要大約 100 個線性方程的解,這就強調了求解器可伸縮性的重要性。骨骼結構中初始屈服點的定位使得非線性分析的收斂變得更加具有挑戰性(參見圖 3)。
表 2:6.4-3 版直接稀疏求解器性能
CPU 數 |
求解時間(秒) |
加速 |
總時間(秒) |
|
1 |
554 |
1.00 |
1,348 |
|
2 |
295 |
1.88 |
1,107 |
|
4 |
171 |
3.24 |
945 |

圖 3:在 2% 壓縮應變情況下邊長為 2.5 毫米立方體的μFE 模型的骨骼結構局部應力分布圖
圖 4 是根據表觀應變(樣本長度的變化/原始樣本長度)作出的表觀應力(外力/橫截面面積(25 平方毫米))圖。初始屈服點定義為偏移量達到 0.2% 的點。與試驗數據(參見參考文獻 4)類似,壓縮時的屈服應變比拉伸時的大。
表 3:不同模型組合的屈服應變
幾何非線性 |
加載模式 |
|
|
拉伸 |
壓縮 |
|
|
考慮 |
0.61 |
0.78 |
|
不考慮 |
0.59 |
0.86 |
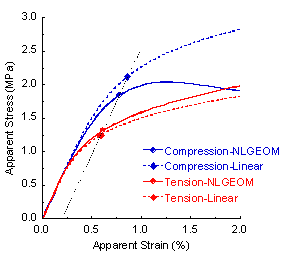
圖 4:四個非線性分析的應力應變關系圖幾何非線性在壓縮時引起軟化,拉伸時引起硬化標記顯示由 0.2% 偏移量方法(點劃線)確定的初始屈服點
雖然組織材料在硬化,但當考慮幾何非線性時,很明顯地觀察到有軟化發生(參見圖 4)。另外屈服應變與試驗測量結果類似,特別是壓縮的情況下(參見參考文獻 4)。這些結果表明在拉伸和壓縮時骨小梁組織有著不同的屈服特性,應該把 μFE 模型和幾何非線性結合起來,精確地模擬骨小梁的平面屈服特性。
相關文章
- 2021-09-08BIM技術叢書Revit軟件應用系列Autodesk Revit族詳解 [
- 2021-09-08全國專業技術人員計算機應用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應用 制表、數據處理及宏應用PDF下載
- 2021-08-30從零開始AutoCAD 2014中文版機械制圖基礎培訓教程 [李
- 2021-08-30從零開始AutoCAD 2014中文版建筑制圖基礎培訓教程 [朱
- 2021-08-30電氣CAD實例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風暴2:Maya影像實拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術設計案例教程中文版AutoCAD 建筑設計案例
- 2021-08-29環境藝術制圖AutoCAD [徐幼光 編著] 2013年PDF下載
- 2021-08-29機械AutoCAD 項目教程 第3版 [繆希偉 主編] 2012年PDF