在曲面繪制方面，雖然Matlab生成的圖形不能直接用于機械設計，但其繪圖的機理都是一樣的，都是由點生成線，再生成面，區別是Matlab以直代曲，ProE一般生成曲線采用插值，因此，只需要把在MATLAB中繪制的公式曲線、曲面上所有的點坐標數據都提取出來，若能讓ProE正確識別，那么我們就可以在其中精確地繪制這些曲線、曲面了。經過嘗試,利用Matlab 取得生成曲面需要的數據,將結果存儲于. ibl 中，利用ProE 可以直接從. ibl 文件生成曲線這一功能，直接生成曲線，進而生成曲面即可

     操作方法,在ProE 中選擇“插入”>“基準”>“曲線”或單擊基準工具欄上曲線按鈕, 選擇“從文件”, 然后選擇“完成”, 再創建或選擇一個曲線參照坐標系, 就可以在出現的窗口中選擇要打開的.ibl 文件, 再點擊“確定”后曲線就生成了。由.ib l 文件創建曲線的最大優點是改變方便。曲線數據如有改動, 只要修改一下. ibl 文件然后對曲線用“重定義”的方法重新指定文件即可。還有一個優點是可以用一個文件生成多條曲線, 在零件的目錄樹上可以顯得非常簡潔。

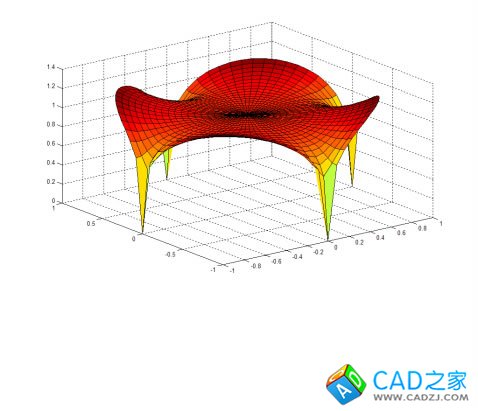
下面是實現過程，以馬鞍形為例

(1)利用MATLAB得到公式曲面數據

    1)在MATLAB中繪制出曲面

    M文件

      [th,r]=meshgrid((0:5:360)*pi/180,0:.05:1); %在極坐標系下設置一個73×21的網格矩陣，
　　　　[X,Y]=pol2cart(th,r); %轉化為笛卡兒坐標系%
    Z=X+i.*Y;
    F=abs((Z.^4-1).^(1/4));
    surf(X,Y,F); %顯示曲面的立體圖形%
    S=[X(:) Y(:) F(:)]; %把X、Y、F 3個矩陣中的數據存儲到矩陣S中%
    b=size(S);
    S=[floor(1:b(1,1));S']';
    save flcxq.ibl S -ascii

 

下面按照ProE生成混合曲線的文件格式對上面生成的結果進行些許修改。

具體參見ProE幫助文檔

closed
arclength

begin section
begin curve
  1.0000000e+000  0.0000000e+000  0.0000000e+000  1.0000000e+000
  2.0000000e+000  5.0000000e-002  0.0000000e+000  9.9999844e-001
  3.0000000e+000  1.0000000e-001  0.0000000e+000  9.9997500e-001
  4.0000000e+000  1.5000000e-001  0.0000000e+000  9.9987341e-001
  5.0000000e+000  2.0000000e-001  0.0000000e+000  9.9959976e-001
  6.0000000e+000  2.5000000e-001  0.0000000e+000  9.9902200e-001
  7.0000000e+000  3.0000000e-001  0.0000000e+000  9.9796882e-001
  8.0000000e+000  3.5000000e-001  0.0000000e+000  9.9622714e-001
  9.0000000e+000  4.0000000e-001  0.0000000e+000  9.9353763e-001
  1.0000000e+001  4.5000000e-001  0.0000000e+000  9.8958692e-001
  1.1000000e+001  5.0000000e-001  0.0000000e+000  9.8399484e-001
  1.2000000e+001  5.5000000e-001  0.0000000e+000  9.7629370e-001
  1.3000000e+001  6.0000000e-001  0.0000000e+000  9.6589456e-001
  1.4000000e+001  6.5000000e-001  0.0000000e+000  9.5203095e-001
  1.5000000e+001  7.0000000e-001  0.0000000e+000  9.3366077e-001
  1.6000000e+001  7.5000000e-001  0.0000000e+000  9.0928394e-001
  1.7000000e+001  8.0000000e-001  0.0000000e+000  8.7656997e-001
  1.8000000e+001  8.5000000e-001  0.0000000e+000  8.3148717e-001
  1.9000000e+001  9.0000000e-001  0.0000000e+000  7.6578710e-001
  2.0000000e+001  9.5000000e-001  0.0000000e+000  6.5626965e-001
  2.1000000e+001  1.0000000e+000  0.0000000e+000  0.0000000e+000

　　　　　　　......

生成效果圖如下;