所謂結(jié)構(gòu)拓?fù)鋬?yōu)化是指結(jié)構(gòu)中材料的布局優(yōu)化，它能為形狀/尺寸優(yōu)化提供新穎、合理的初始設(shè)計。連續(xù)體結(jié)構(gòu)拓?fù)鋬?yōu)化理論始于20世紀(jì)80年代末，經(jīng)過不斷發(fā)展和完善，現(xiàn)已廣泛應(yīng)用于航空、航天、機(jī)械制造、復(fù)合材料設(shè)計等諸多領(lǐng)域。連續(xù)體拓?fù)鋬?yōu)化方法中影響最大、應(yīng)用最廣的是變密度法(Solid Isotropic Microstructures with Penalization簡稱SIMP法)。目前，該方法已集成于多種結(jié)構(gòu)分析軟件，如HyperWorks、ANSYS等。

　　朱軍祚等最早利用ANSYS中拓?fù)鋬?yōu)化模塊探討了水工鋼閘門的設(shè)計問題。該工作僅停留在理論探討層面。為了使得拓?fù)鋬?yōu)化能夠有效地指導(dǎo)水工結(jié)構(gòu)設(shè)計，尤其是弧形鋼閘門的設(shè)計中。本文以一個現(xiàn)實的露頂式弧形鋼閘門設(shè)計方案為例，采用分步拓?fù)鋬?yōu)化方法進(jìn)行了新型弧形鋼閘門結(jié)構(gòu)設(shè)計方法的探索。

　　1 連續(xù)體拓?fù)鋬?yōu)化概念

　　1.1 SIMP方法的數(shù)學(xué)描述

　　在SIMP方法中，若結(jié)構(gòu)分析材料有限元方法進(jìn)行，則單元的偽密度為單元的設(shè)計變量，偽密度取值范圍是(0 1]。偽密度趨于零表示單元中無材料，等于1則表示單元中材料無空隙。偽密度介于0和1之間的單元稱為中間密度單元。為了便于提取邊界，需減少中間密度單元的個數(shù)，因此往往采用密度懲罰的辦法，即單元中材料的彈性模量與偽密度的p次方成正比。p即為密度懲罰因子，本文取其值為3。同時，為了避免棋盤格等數(shù)值不穩(wěn)定現(xiàn)象的出現(xiàn)，需對目標(biāo)函數(shù)的敏度做濾波處理。

　　通常，剛度優(yōu)化設(shè)計問題可用下式表述：

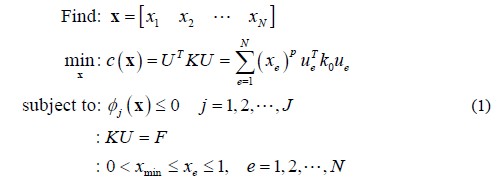
　　其中，U和F為全局位移向量和力向量，K為全局剛度矩陣，即結(jié)構(gòu)總剛度陣，ue和ke是單元位移矢量和單元剛度矩陣，設(shè)計變量xe為單元的偽密度，xmin是偽密度下限(不為零，以避免結(jié)構(gòu)總剛度陣奇異)，N為設(shè)計域內(nèi)單元的個數(shù)，p是懲罰因子，φj為約束函數(shù)，如體積約束、位移約束、應(yīng)力約束、屈曲約束和頻率約束等。J為約束函數(shù)個數(shù)。1.2 結(jié)構(gòu)拓?fù)鋬?yōu)化的實現(xiàn)本文采用有限元軟件HyperWorks的拓?fù)鋬?yōu)化功能實現(xiàn)結(jié)構(gòu)拓?fù)鋬?yōu)化分析。

　　2 應(yīng)用實例

　　2.1 工程概況

　　某水電站溢洪道工作弧門結(jié)構(gòu)布置圖如圖1 a所示工作閘門結(jié)構(gòu)設(shè)計為雙腹板主橫梁、斜支臂結(jié)構(gòu)形式(支臂截面為箱型)，閘門結(jié)構(gòu)各個部件布置情況見圖2 所示。

　　(i) 閘門布置參數(shù)

　　孔口高度：20.0m

　　閘門高度：20.333m

　　底檻高程：455.167m

　　支鉸高程：466.50m

　　弧門半徑：24.00m

　　工作弧門20×20.333m2，設(shè)計水頭19.833m，總水壓力約39000KN。

　　(ii) 板件厚度

　　見附錄1。

　　(iii) 材料參數(shù)

　　閘門所用材料為Q345B鋼材，彈性模量為206GPa，泊松比為0.3，密度ρ=7800kg/m3。【結(jié)構(gòu)總重約273噸】

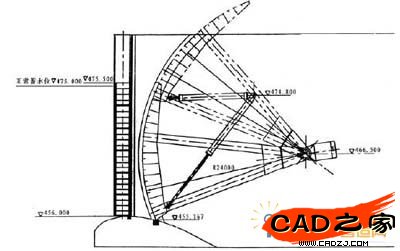
　　圖 1 工作弧門結(jié)構(gòu)布置圖

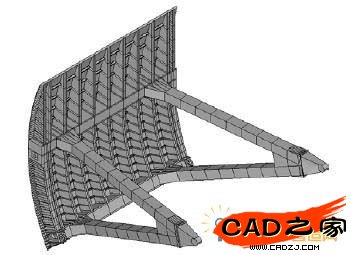
　　圖 2 弧門結(jié)構(gòu)的傳統(tǒng)設(shè)計方案

　　2.2 設(shè)計步驟

　　大量的分析表明，如果采用三維實體結(jié)構(gòu)直接進(jìn)行拓?fù)鋬?yōu)化，得到的結(jié)果往往難以制造，甚至無法為結(jié)構(gòu)設(shè)計提供新思路。為此，本文采用逐步拓?fù)鋬?yōu)化的方法將弧形鋼閘門看作是由三個主要部件，即兩個支臂、擋水面板和支撐擋水面板的框架，構(gòu)成的三維結(jié)構(gòu)。在設(shè)計該結(jié)構(gòu)的過程中主要包括以下幾個步驟：

　　1) 支臂的設(shè)計方案;

　　2) 支撐框架中縱向肋的布局;

　　3) 支撐框架中橫向肋的布局;

　　4) 構(gòu)造鋼閘門的整體結(jié)構(gòu)并安全性分析;

　　5) 其他工況下的結(jié)構(gòu)安全性校核。

　　2.3 設(shè)計過程

　　為了便于計算及描述，全局坐標(biāo)系設(shè)定為直角坐標(biāo)系(OXYZ)：X向為從坐標(biāo)原點沿水流方向指向上游為X軸正方向;從坐標(biāo)原點豎直向上為Y軸正方向;過坐標(biāo)原點、與過支鉸中心線平行并指向右支鉸的方向為Z軸正方向。

　　2.3.1 支臂的設(shè)計方案

　　支臂的確定包括支臂的位置、拓?fù)洹⑿螤詈统叽绲拇_定。該閘門的原始設(shè)計形式采用的是露頂式直支臂弧形鋼閘門，支臂截面形式為箱型，支臂與弧形擋水面正交。目前仍設(shè)定支臂所在平面與擋水面板所在曲面正交。

　　I: 主支臂的位置

　　兩組支臂的位置可通過如圖3 所示的外伸等直梁中支撐的位置確定。易知，在均布荷載作用下，為保證梁在支撐處的轉(zhuǎn)角為零，利用材料力學(xué)中梁的變形分析可知支座距離中心的長度()占總長(#p#分頁標(biāo)題#e#

)的0.293。因此當(dāng)弧形鋼閘門的跨度為20000mm時，支臂中心應(yīng)距離擋水面板縱對稱面5860mm處。

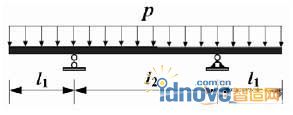
　　圖 3 均布荷載作用下的外伸梁模型

　　II: 主支臂的拓?fù)洹⑿螤詈统叽?/p>

　　為了便于制造，在確定支臂拓?fù)洹⑿螤詈统叽鐣r，現(xiàn)將原三維結(jié)構(gòu)轉(zhuǎn)化為二維分析，靜水壓力也相應(yīng)地凝縮到二維邊界。根據(jù)實際工程中鋼閘門的側(cè)視圖，取二維的初始設(shè)計域為一個扇形(見圖4 a)，扇形面的弧形半徑即為工作弧門半徑。

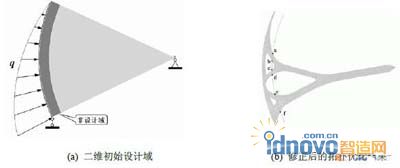
　　圖 4 支臂拓?fù)鋬?yōu)化模型及結(jié)果

　　在確定支臂拓?fù)鋾r，工作弧門外表的擋水面板應(yīng)設(shè)為非設(shè)計域。支臂與擋水面板之間應(yīng)有縱向加強(qiáng)肋，以確保擋水面板受力均勻，變形小。此時，也設(shè)定加強(qiáng)肋所占區(qū)域為非設(shè)計域。因此，確定支臂拓?fù)洹⑿螤畹亩S初始設(shè)計中，非設(shè)計域的厚度由擋水面板的厚度和加強(qiáng)肋的厚度組成。該值需重新確定，其估算公式為：

　　其中：參數(shù)α取值范圍為[10 20]，擋水面板的跨度L為200000mm，箱型支臂中縱向面內(nèi)板的厚度D為4×30mm=120mm，擋水面板的厚度TO的初始值為16mm。同時，參考規(guī)范[1]，初步將二維初始設(shè)計中非設(shè)計區(qū)域深度取為1800mm。

　　扇形設(shè)計域中圓心位置及位移約束可按照圖1中參數(shù)確定。擋水面板上的荷載q，即靜水壓力按滿載(最不利工況)設(shè)定。圖4 a所示的初始設(shè)計域中，材料選取Q345B鋼材。拓?fù)鋬?yōu)化的目標(biāo)是結(jié)構(gòu)柔度最小，約束條件為優(yōu)化后的結(jié)構(gòu)體積(即材料用量)占總體積的14%(即臨界體積率為14%)。本次優(yōu)化過程中暫不考慮結(jié)構(gòu)自重，否則自重占據(jù)荷載主體，最終結(jié)構(gòu)不利于抵擋水壓力。圖4 b為優(yōu)化后并經(jīng)修正得到的支臂形狀(具體尺寸可參見附錄2)。

　　2.3.2 縱向肋的布局方案

　　縱向肋是構(gòu)成擋水面板的支撐框架的一部分。其布局方案包括，結(jié)構(gòu)中縱向肋的數(shù)量、位置以及不同位置處縱向肋的深度。

　　為了獲得縱向肋的布局方案，取三維結(jié)構(gòu)中任意一個橫截面(與圖4 a中結(jié)構(gòu)正交)，其模型如圖3 中外伸梁，但梁的深度為2000mm，即略高于縱向肋最大深度(1800mm)，以便消除自由度約束處局部剛度過大現(xiàn)象;寬度為10000mm，即整體結(jié)構(gòu)的一半。梁下位移約束設(shè)定為1100mm，即支臂的寬度，荷載為均布壓力。其結(jié)構(gòu)分析模型的一半為圖5 a所示。在優(yōu)化過程中，僅將擋水面板設(shè)定為非設(shè)計域，結(jié)構(gòu)柔度最小為優(yōu)化目標(biāo)，具有體積約束(臨界體積率為20%)。對其進(jìn)行拓?fù)鋬?yōu)化，優(yōu)化后得到弧形擋水面中縱向肋數(shù)量、位置及深度(如圖5 b所示)。

　　同時參照規(guī)范對部分尺寸進(jìn)行了修正，得到結(jié)構(gòu)初始設(shè)計的具體尺寸，如表1所示。所有縱向肋均采用工字鋼。由此可以建立縱向肋的布局方案(參見圖5 c)。

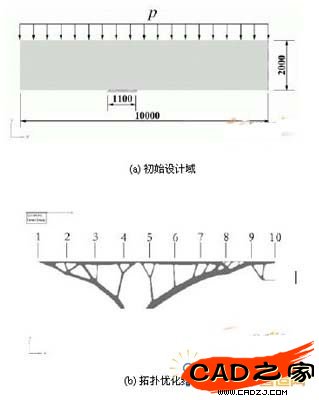
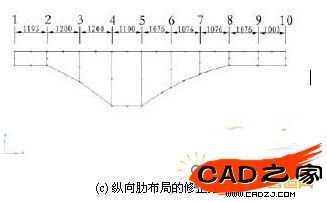
　　圖 5 縱向肋布局優(yōu)化及結(jié)果

　　表 1 縱向肋的深度

　　2.3.3 橫向肋的布局方案

　　橫向肋包括結(jié)構(gòu)中部肋和邊界肋。邊界肋即為擋水面板上下兩條邊界上布設(shè)的肋。而中部布設(shè)的肋需通過拓?fù)鋬?yōu)化分析獲得。

　　圖 6 為橫向肋拓?fù)鋬?yōu)化的初始設(shè)計域示意圖。為了降低計算量，將支臂所在非設(shè)計區(qū)域去掉，交界處代之以固定位移約束。圖6 b和6 c為橫向肋拓?fù)鋬?yōu)化的初始設(shè)計域三維視圖。

　　對整體三維結(jié)構(gòu)(見圖6 c)進(jìn)行拓?fù)鋬?yōu)化，在優(yōu)化過程中，僅將擋水面板設(shè)定為非設(shè)計域，結(jié)構(gòu)柔度最小為優(yōu)化目標(biāo)，具有體積約束(臨界體積率為10%)，并沿Z向施加生產(chǎn)制造(碾壓成型)約束。

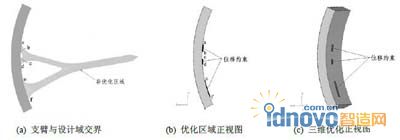
　　圖 6 橫向肋布局優(yōu)化初始設(shè)計

　　拓?fù)鋬?yōu)化后得到弧形擋水面的支撐框架中橫向肋位置的初始設(shè)計方案，如圖7 所示。圖7 b中1號線上側(cè)有材料，但沒有布置肋。

　　修正后各個1-8號橫向肋與0號線夾角的角度(參見表2)。因橫向肋與縱向肋相互卡接，縱向肋的間距小，所以橫向肋均采用矩形截面鋼(平面鋼板)。由此建立橫向肋的布局方案(參見圖7 b)。

　　 #p#分頁標(biāo)題#e#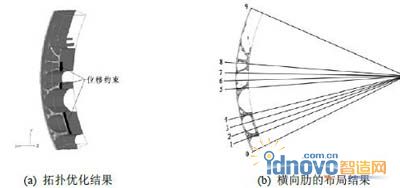

　　圖 7 橫向肋布局優(yōu)化及結(jié)果

　　表 2 橫向肋的布置角度

　　此外，除了上述橫向肋外，擋水面板的上下邊界也需布設(shè)橫向肋。這兩根橫向肋(0號和9號)無卡槽，不僅能提高結(jié)構(gòu)剛度、加強(qiáng)縱向肋的穩(wěn)定性，同時也有利于提高結(jié)構(gòu)強(qiáng)度。尤其是底部橫向肋(0號)上與支臂交叉處將布設(shè)吊耳。因此，擋水面板的支撐框架內(nèi)含有10根橫向肋。

　　2.3.4 建立結(jié)構(gòu)初始設(shè)計模型并做安全性分析

　　根據(jù)以上分步拓?fù)鋬?yōu)化結(jié)果，可以得到模型的支臂、縱向肋和橫向肋等部分的布局方案。擋水面板的支持框架中含19根縱向肋(10號縱向肋處在鋼閘門的對稱面內(nèi))。利用各部件的設(shè)計方案建立弧形鋼閘門的三維模型(參見圖8 )。各部件初始尺寸可參見附錄1。

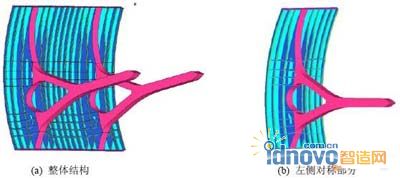
　　圖 8 弧形鋼閘門整體結(jié)構(gòu)初始設(shè)計

　　滿載工況是指結(jié)構(gòu)考慮自重的情況下，工作水頭達(dá)到設(shè)計水頭(19.833m)時結(jié)構(gòu)的受力狀態(tài)。非滿載時，結(jié)構(gòu)中除自重外，還可能存在不同水頭下的靜水壓力荷載。

　　分析過程中，因支鉸處沒有設(shè)計支撐細(xì)節(jié)，因此支鉸及附近1.8m范圍內(nèi)的應(yīng)力將不作為參考。

　　(i)剛度校核

　　滿載條件下結(jié)構(gòu)分析得到位移云圖(見圖9)。可發(fā)現(xiàn)，弧形擋水面的上部位移相對較大，而實際中弧形擋水面上部受到的荷載作用是相對較小的。位移最大值為65.2mm，位于擋水面上部的兩個角端位置;兩側(cè)縱向肋中部和底部位移較小且比較均勻，介于10~20mm之間，底部最低點的位移為14.7mm;面板中部偏下和底部位移較大，介于25~37mm之間。

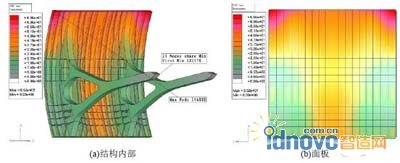
　　圖 9 結(jié)構(gòu)位移云圖

　　(ii)強(qiáng)度校核

　　滿載條件下結(jié)構(gòu)的應(yīng)力云圖如圖10所示。從圖中可以看出，應(yīng)力高于345MPa的區(qū)域是支鉸附近區(qū)域范圍內(nèi)，原因在于在分析時僅作線彈性分析。但該部分需做圓柱鉸，細(xì)節(jié)改變后受力狀態(tài)也會改變。支臂中除支撐點外的最大應(yīng)力出現(xiàn)在上部主干直支臂與分支臂過渡區(qū)(如圖10中A點)，最大應(yīng)力值為260MPa，支臂的其余部分應(yīng)力均小于210MPa;縱向肋中應(yīng)力最大的位置是支臂連接的外側(cè)縱向肋(4號縱向肋)的下部，與面板和橫向肋連接的局部范圍內(nèi)(如圖10中B點)其值為494MPa(大于345MPa)，需要做局部加強(qiáng)處理。除了與橫向肋連接處應(yīng)力相對較大外，縱向肋的其余部分應(yīng)力值均小于170MPa;橫向肋中應(yīng)力最大的位置是2號橫向肋與支臂內(nèi)側(cè)連接處(如圖10中C點)，其值為332.6MPa，除了與支臂連接處應(yīng)力相對較大外，橫向肋的其余部分應(yīng)力值均小于175MPa;擋水面板中應(yīng)力最大的位置是4號縱向肋與面板的下部連接處，其值為308.8MPa，擋水面板中除最下層面板外，面板的其余部分應(yīng)力值均小于205MPa。

　　圖 10 結(jié)構(gòu)應(yīng)力云圖

　　(iii)屈曲穩(wěn)定性校核

　　對所建立的模型施加實際的約束和荷載之后，進(jìn)行模態(tài)分析。一階模態(tài)如圖11所示，首先進(jìn)入失穩(wěn)的位置在上部支臂與7號橫向肋交界附近，對應(yīng)的屈曲臨界荷載因子為3.514(遠(yuǎn)大于1.0)。因重力為不變荷載，因此真實值大于3.514。

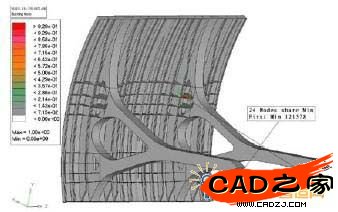
　　圖 11 閘門的一階模態(tài)

　　(iv)動力穩(wěn)定性校核

　　通常，水流激勵頻率在[0 3]之間。為了避免結(jié)構(gòu)發(fā)生共振，需避開此區(qū)間。對上述結(jié)構(gòu)進(jìn)行自振分析。一階頻率(基頻)為4.266，遠(yuǎn)離水流頻率。因此結(jié)構(gòu)滿足動力穩(wěn)定性。2.3.5其他工況下的結(jié)構(gòu)安全性校核(i)非滿載工況表3給出了不同工況下結(jié)構(gòu)中應(yīng)力和位移最大值及所處位置。不難發(fā)現(xiàn)，滿載時底部四號縱向肋應(yīng)力超過許用應(yīng)力，需做局部加強(qiáng)。

　　表3 不同水頭下結(jié)構(gòu)中最大應(yīng)力及最大位移

　　(ii)滿載下吊耳工作工況

　　吊耳工作時可看作是將吊耳所在位置上的節(jié)點沿Y向指定一個很小的位移值。底部橫向肋上其他點的位移約束全部去掉。結(jié)構(gòu)的最大位移值為66.5mm，位于面板上部中間;結(jié)構(gòu)中除支鉸外的其他部分受力比較均勻，應(yīng)力值均小于259MPa。

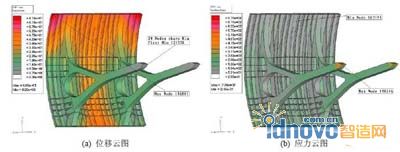
　　圖 12 吊耳工作時滿載結(jié)構(gòu)位移及應(yīng)力分布#p#分頁標(biāo)題#e#

　　3 結(jié)論

　　利用優(yōu)化方法并結(jié)合實例設(shè)計了新型弧形閘門，給出了設(shè)計露頂式弧形鋼閘門的設(shè)計步驟。在確保結(jié)構(gòu)的強(qiáng)度、剛度和穩(wěn)定性等性能指標(biāo)具有一定安全裕度條件下，經(jīng)優(yōu)化后結(jié)構(gòu)重量較傳統(tǒng)設(shè)計減重約26%。結(jié)構(gòu)自重大大降低的優(yōu)點在于：節(jié)省材料、降低造價、便于安裝和操作。