近年來(lái),數(shù)控自動(dòng)編程發(fā)展迅速,有很多以計(jì)算機(jī)圖形學(xué)為基礎(chǔ)的自動(dòng)編程軟件(如MasterCAM、UG等),有效地解決了幾何造型、零件幾何形狀的顯示、交互式設(shè)計(jì)、修改以及刀具軌跡生成等問(wèn)題,使得CAD/CAM逐步走向一體化。然而,數(shù)控自動(dòng)編程必須增加計(jì)算機(jī)硬件和軟件系統(tǒng),增加了設(shè)備投資;自動(dòng)編程軟件的學(xué)習(xí)以及熟練運(yùn)用需要一定的時(shí)間,需要一定的計(jì)算機(jī)知識(shí)和一定的機(jī)械基礎(chǔ)知識(shí),而且現(xiàn)代的編程軟件為了做到功能全面,增加了許多新的加工概念和方式,軟件包整體比較復(fù)雜和龐大,若想熟練掌握運(yùn)用存在一定困難;自動(dòng)編程產(chǎn)生的加工程序一般比較長(zhǎng),同樣的零件,自動(dòng)編程的程序可能是手工編程的程序長(zhǎng)度的幾倍甚至幾十倍,其加工時(shí)間相應(yīng)地會(huì)成倍或成幾十倍地增長(zhǎng),這是其無(wú)法修正的根本缺陷。因此,對(duì)于小批量生產(chǎn)、形狀相對(duì)簡(jiǎn)單的外冷噴油嘴的橢球面部分來(lái)說(shuō),采用手工編程,利用逼近圓的方法編寫C語(yǔ)言程序,把橢球面用球面來(lái)近似,計(jì)算出若干個(gè)點(diǎn),最終通過(guò)這些點(diǎn)編制外冷噴油嘴的橢球面部分的數(shù)控程序,加工形成橢球面輪廓的方法是可行的,既節(jié)約了成本,也節(jié)省了加工時(shí)間。
一、橢球面的逼近處理
對(duì)于噴油嘴的橢球面部分,數(shù)學(xué)處理的任務(wù)是用直線段或圓弧段去逼近非圓輪廓。噴油嘴的零件圖如圖1所示。

在車床上車削橢球面,車床系統(tǒng)只有直線插補(bǔ)和圓弧插補(bǔ)功能,沒(méi)有橢圓曲線插補(bǔ)功能。因此,對(duì)于橢圓曲線的逼近也有兩種方式。一是直線逼近:如果曲線方程比較簡(jiǎn)單,又不準(zhǔn)備做理論誤差驗(yàn)算,那么借助計(jì)算器就可以完成,但直線逼近的誤差較大,只適用于比較粗糙的加工。另一種是用圓弧逼近。圓弧逼近一般應(yīng)借助微機(jī)來(lái)完成,也有兩種逼近方式。
一種方法是先按估計(jì)分段,編寫一個(gè)程序作逼近,然后再編一個(gè)程序驗(yàn)算誤差,如果算出的誤差超過(guò)允許值,再回過(guò)來(lái)增加分段數(shù),反復(fù)幾次,直到誤差略小于允許值為止。此法操作起來(lái)雖麻煩一些,但兩個(gè)程序都比較簡(jiǎn)單。另一種方法是邊逼近邊計(jì)算誤差,使算出的逼近圓弧與實(shí)際輪廓間的誤差總是小于或等于某個(gè)允許值。
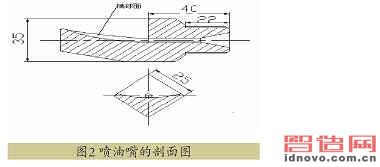
這樣的程序雖然復(fù)雜一些,但機(jī)上操作就簡(jiǎn)單多了。圖2所示的是噴油嘴的剖面圖。
在噴油嘴橢球面部分的圓弧逼近中,本文選擇等誤差逼近方法,它能以最少的逼近圓
弧段來(lái)獲得最高的逼近精度。如能把每段逼近圓弧與橢圓間的距離限制在1μm之內(nèi),那么由編程引起的理論誤差就可以忽略不計(jì)了。編制如此精密逼近的數(shù)控加工程序,關(guān)鍵是作等誤差逼近計(jì)算。只要算出每個(gè)逼近圓的數(shù)據(jù),編寫加工程序就很方便了。
1.方法的選擇
對(duì)需要加工的那段橢圓作等分,如圖3所示。在AB上沿逆時(shí)針?lè)较蛉↑c(diǎn),依次為U1,U2,…,Un。一種取法是讓相鄰兩點(diǎn)間的x向距離相等,然后用橢圓方程算出各點(diǎn)的y值。這種取法的缺點(diǎn)是各區(qū)段弧長(zhǎng)相差甚大,而且曲線段越長(zhǎng)的區(qū)段的曲率變化越大。
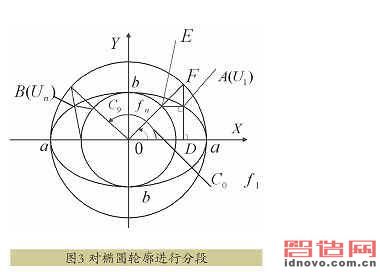
采用另外一種取法,即讓相鄰兩點(diǎn)的參數(shù)值相等。橢圓的參數(shù)方程如式(1)所示。
看一下變量中的幾何意義。先以a、b為半徑作兩個(gè)同心圓,再作半徑OF,交于點(diǎn)E。從F點(diǎn)作X軸的垂線FD,再?gòu)?E點(diǎn)作X軸的平行線,并與FD交于A。把∠FOX作為變量,用Ф表示。把點(diǎn) A確定在加工起點(diǎn),并用U1(x1,y1)表示,令其相應(yīng)的參數(shù)角為Ф1。給參數(shù)一個(gè)增量Δ Ф,令Ф1+ΔФ=Ф2,與Ф2相應(yīng)的點(diǎn)用U2(x2,y2)表示,那么用此法沿逆時(shí)針依次取U3,U4,…,Un,Un應(yīng)到達(dá)或略超過(guò)加工終點(diǎn)B,這種用相同參數(shù)增量取的點(diǎn)群,其相鄰兩點(diǎn)間的弧長(zhǎng)相差不大。
2.逼近圓的一般概念和計(jì)算
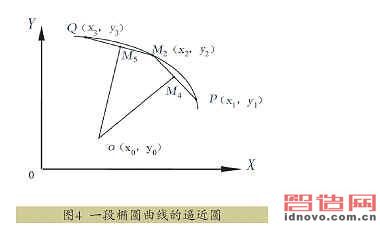
在上述橢圓上任取兩點(diǎn)P(x1,y1)、Q(x3,y3),它們的參數(shù)角分別為C1、C3;在橢圓輪廓的PQ間取一點(diǎn)M2(x2,y2),使其對(duì)應(yīng)的參數(shù)C2=(C1+C3)/2。令PM2、M2Q的中點(diǎn)分別為M4(x4,y4)和M5(x5,y5)。從M4、M5分別作PM2、M2Q的垂線,這兩條垂線交于O(x0,y0),O就是P、M2、Q三點(diǎn)決定的圓的圓心,亦即與PQ間橢圓曲線逼近的圓的圓心,OP是圓的半徑。根據(jù)已知條件來(lái)計(jì)算這個(gè)逼近圓。如圖4所示,直線OM4和OM5的方程聯(lián)立,解得這個(gè)圓的方程如式(2)所示。
3.逼近圓誤差的一般計(jì)算
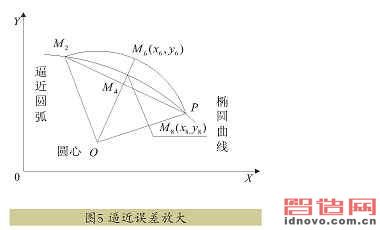
把圖4的右半部分放大,作成圖5。令 OM4的延長(zhǎng)線與圓的交點(diǎn)為M6(x6,y6)、與橢圓的交點(diǎn)為M8(x8,y8)。可以把M6M8的長(zhǎng)度看作是這部分的最大誤差。為求M6M8的長(zhǎng)度,先得計(jì)算M6、M8點(diǎn)的坐標(biāo)值。M6的坐標(biāo)是直線方程OM4和圓方程(2)組成的方程組的解。M8的坐標(biāo)是由直線方程OM6和橢圓方程組成的方程組的解,式中的正負(fù)選擇與x4的正負(fù)號(hào)相同后,經(jīng)過(guò)計(jì)算M6M8的長(zhǎng)度為
將右側(cè)PM2間的最大誤差D1與允許誤差作比較,判別是否超差。再用同樣的方法算出左側(cè)M2Q間的最大誤差D2,將它與允差作比較,判別是否超差。只有左右兩部分均未超差才能認(rèn)定截取的PQ間沒(méi)有超差。
4.實(shí)用逼近圓的選擇
如圖3所示,先把第1、3點(diǎn)U1、U3分別作為P、Q點(diǎn),即取P=1、Q=3。按上述方法作第一個(gè)逼近圓的計(jì)算、誤差計(jì)算和判別。如未超差,就改取U1、U4作為P、Q點(diǎn),即取P=1、Q=4作第二個(gè)圓,再進(jìn)行相應(yīng)的計(jì)算和判別。只要不超差,圓就繼續(xù)試作下去。如作到第W個(gè)圓算出超差,那么前一個(gè)圓,即過(guò)P=1、Q=W-1點(diǎn)的圓,就是找到的第一個(gè)實(shí)用逼近圓。這個(gè)實(shí)用逼近圓Q點(diǎn)的坐標(biāo)、圓心相對(duì)于P點(diǎn)的X、Y向距離I、J和圓半徑,都是有用的數(shù)據(jù)。
接著找第二個(gè)實(shí)用逼近圓。將第一個(gè)實(shí)用逼近圓弧的終點(diǎn) Q,即(Q=W-1)作為新的P點(diǎn),緊接著的下一個(gè)點(diǎn)作為新的Q點(diǎn),重新開(kāi)始作第一個(gè)圓,經(jīng)計(jì)算如不超差,就將Q再往前取一點(diǎn),作第二個(gè)圓,直到作到第L個(gè)圓算出超差,那么前一個(gè)圓( L-1)就是找到的第二個(gè)實(shí)用逼近圓。這樣依次找下去,直到某個(gè)實(shí)用逼近圓弧的終點(diǎn)達(dá)到或超過(guò)橢圓的加工終點(diǎn)B為止,找到若干個(gè)實(shí)用逼近圓。
二、C語(yǔ)言程序的編寫
每個(gè)參數(shù)角增量取0.00063弧度比較適當(dāng),這意味著整個(gè)圓要分成近萬(wàn)段。這就要計(jì)算近萬(wàn)個(gè)圓和近兩萬(wàn)個(gè)誤差,顯然這必須借助計(jì)算機(jī)來(lái)實(shí)現(xiàn)。根據(jù)以上的計(jì)算方法和思路,編制了C語(yǔ)言程序,部分程序如下.
#include
#include
main()
{
double x,y,x0,y0,
…
..,a,b,r,d1,d2;定義各個(gè)參數(shù)。
Int q;
c0=3*1.570796;初始點(diǎn)參數(shù)角值。
c1=c0;
c3=c0+q*0.00063;
c2=(c1+c3)/2;
x1=a*cos(c1);
y1=b*sin(c1);
x3=a*cos(c3);
y3=b*sin(c3);
……
scanf("%f,%f,%f”,&a,&b,&q);輸入橢圓的長(zhǎng)軸,短軸以及點(diǎn)數(shù)
printf("%f,%f,%f,%f,%f",a,bx, y,r,d1,d2);輸出逼近圓x,y的坐標(biāo)值以及圓的半徑,
d1,d2為是否超差,如超差,該值舍去
}
三、數(shù)控程序的編制及加工過(guò)程的實(shí)現(xiàn)
該零件在CAK6150DI臥式數(shù)控車床上加工,該機(jī)床采用FANUC數(shù)控系統(tǒng),這里需要注意一點(diǎn),用C語(yǔ)言程序計(jì)算出來(lái)的x、y、r等值需要轉(zhuǎn)換成機(jī)床上的加工代碼,x值即是機(jī)床的z向坐標(biāo)值,y值的2倍就是數(shù)控程序x軸的坐標(biāo)值。編制的部分?jǐn)?shù)控程序代碼如下。
粗車部分程序:
G00 x52.34,z45.0;
G03 x59.23,z44.86,
R58.53,F0.15;
G03 x65.56,z38.01,
R68.61,F0.15;
G03 x71.09,z29.74,
R79.12,F0.15;
G03 x75.41,z19.55,
R89.06,F0.15;
G03 x77.58,z6.2,R96.66,F0.15;
…
精車部分程序:
…
G03 x59.60,z45.0,R58.91,F0.08;
G03 x65.95,z38.10, R69.03,F0.08;
G03 x71.47,z29.83, R79.55,F0.08;
G03 x75.80,z19.63, R89.49,F0.08;
G03 x78.0,z5.0, R97. 10,F0.08;
G01 x36.5z5.0, F0.08;
G00x36.5z50.0;
T0100;
M05;
M30;
四、結(jié)束語(yǔ)
數(shù)控手工編程在任何時(shí)候都是必要的,是編程技術(shù)不可缺少的一部分。中等難度以下零件的手工編程的難點(diǎn)多在于數(shù)值點(diǎn)的計(jì)算和處理,而且手工編程并不排斥計(jì)算機(jī)的應(yīng)用,通用軟件在輔助人工計(jì)算處理圖形節(jié)點(diǎn)、坐標(biāo)數(shù)值點(diǎn)方面極為有效。通常進(jìn)行人工計(jì)算需要花費(fèi)半天甚至一天的圖形,利用編寫程序,在計(jì)算機(jī)上僅用十多分鐘就能完成數(shù)值計(jì)算,而且能保證一定的精度。所以根據(jù)逼近圓的方法,利用計(jì)算機(jī)輔助,最終通過(guò)數(shù)控編程實(shí)現(xiàn)了橢球面的加工。
實(shí)踐證明,這種方法是可行的,不僅節(jié)約了成本,而且節(jié)省了加工時(shí)間。
相關(guān)文章
- 2021-09-08BIM技術(shù)叢書Revit軟件應(yīng)用系列Autodesk Revit族詳解 [
- 2021-09-08全國(guó)專業(yè)技術(shù)人員計(jì)算機(jī)應(yīng)用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應(yīng)用 制表、數(shù)據(jù)處理及宏應(yīng)用PDF下載
- 2021-08-30從零開(kāi)始AutoCAD 2014中文版機(jī)械制圖基礎(chǔ)培訓(xùn)教程 [李
- 2021-08-30從零開(kāi)始AutoCAD 2014中文版建筑制圖基礎(chǔ)培訓(xùn)教程 [朱
- 2021-08-30電氣CAD實(shí)例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風(fēng)暴2:Maya影像實(shí)拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術(shù)設(shè)計(jì)案例教程中文版AutoCAD 建筑設(shè)計(jì)案例
- 2021-08-29環(huán)境藝術(shù)制圖AutoCAD [徐幼光 編著] 2013年P(guān)DF下載
- 2021-08-29機(jī)械A(chǔ)utoCAD 項(xiàng)目教程 第3版 [繆希偉 主編] 2012年P(guān)DF