1 前言
2 圓度的影響因素分析
3 試驗方案
| 水平 | 因素 | Vw (m/min) |
a1 (?m/r) |
a2 (?m/r) |
Sd (mm/r) |
td (mm) |
T (mm3/mm) |
L2 (mm) |
1
30
4
0.5
0.1
0.01
1T0
0.025
2
50.5
8
1
0.2
0.02
5T0
3
83
12
1.8
0.3
0.03
10T0
0.04
|---|
4 磨削圓度與工藝參數關系的建模
- 數學模型假設
- 磨削內圈溝道圓度的逐步回歸建模
- 利用磨削試驗后實測內圈溝道的圓度數據,對上述式(3)線性化的響應函數式(4)進行逐步回歸,即引入重要因素,剔除次要因素(注:F檢驗臨界值取Fa=0.4),直到既不能剔除,又無法再引進變量的情況下逐步回歸計算結束。定出響應函數式(4)各自變量系數的值,再將線性化后的響應函數代換復原,便可得到磨削工藝參數與圓度關系的數學模型為 #p#分頁標題#e#
標準離差s=0.36,相關系數g=0.94,F=26>Fa=0.4R0=0.0623Vw0.442a13.262L20.201De1.08Tb1Sdb2a2b3tdb4
(5)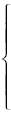 b1=-0.335lna1-0.368lnSd
b2=4.833+1.161lna1+2.178lnSd
b3=-0.233lna1
b4=-0.441lnSd
b1=-0.335lna1-0.368lnSd
b2=4.833+1.161lna1+2.178lnSd
b3=-0.233lna1
b4=-0.441lnSd- 從所建立模型的相關系數和方差分析F檢驗值可知,擬合效果比較滿意,模型是可行的。
- 利用磨削試驗后實測內圈溝道的圓度數據,對上述式(3)線性化的響應函數式(4)進行逐步回歸,即引入重要因素,剔除次要因素(注:F檢驗臨界值取Fa=0.4),直到既不能剔除,又無法再引進變量的情況下逐步回歸計算結束。定出響應函數式(4)各自變量系數的值,再將線性化后的響應函數代換復原,便可得到磨削工藝參數與圓度關系的數學模型為 #p#分頁標題#e#
- 根據前面對磨削圓度影響因素分析,考慮工藝參數間可能存在的交互效應,可假設磨削圓度的數學模型是
式中R0代表圓度值,其余為工藝參數和待定常數,砂輪等效直徑De=dsdw/(d3+dw)。R0= KVwa1a1a2L2a3D4a4Twb1Sdb2ab23tdb4
(3)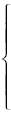 b1=p1+lnVwb1a1b2Tb3Sdb4a2b5Deb6
b2=p2+c1lna1+c2lnSd
b3=p3+dlna1
b4=p4+f1lnSd+f2lntd
b1=p1+lnVwb1a1b2Tb3Sdb4a2b5Deb6
b2=p2+c1lna1+c2lnSd
b3=p3+dlna1
b4=p4+f1lnSd+f2lntd - 通過對式(3)兩邊取對數并進行變量代換后,可線性化為
#p#分頁標題#e#
y=B0+B1x1+B2x2+……+B19x19 (4)
5 結果與討論
- 圖2表示修整砂輪的導程和深度與磨削圓度R0的關系。圖中,當Sd<0.16mm/r時,隨著修整導程Sd的減小,磨削的圓度增大:但是當Sd>0.16mm/r時,磨削的圓度隨修整導程的增大而增大,在Sd=0.16mm/r處,圓度達極小值。隨著砂輪修整深度的增大,磨削的圓度遞增。
- 圖3表示粗進給和細進給磨削深度與磨削圓度的關系。從圖中可知,粗進給和細進給磨削深度的增大,均使磨削的圓度以不同程度減小,其中隨粗進給磨削深度a1的增大,磨削圓度減小的幅度與細進給磨削深度a2有關,a2越大,圓度減小的幅值也越大。
- 圖4表示工件線速度Vw和單位磨除金屬體積T與磨削圓度的關系。磨削的圓度隨工件線速度的增大而增大,而單位磨除金屬體積的變化對磨削的圓度沒有明顯影響。說明在砂輪正常磨損階段,砂輪表面的鋒利狀態不影響圓度。
- 圖5表示等效砂輪直徑De和細進給行程L2與磨削圓度R0的關系。顯然,細進給行程和等效砂輪直徑De的增大,均使磨削的圓度增大。這與第二點的結論一致。
相關文章
- 2021-09-08BIM技術叢書Revit軟件應用系列Autodesk Revit族詳解 [
- 2021-09-08全國專業技術人員計算機應用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應用 制表、數據處理及宏應用PDF下載
- 2021-08-30從零開始AutoCAD 2014中文版機械制圖基礎培訓教程 [李
- 2021-08-30從零開始AutoCAD 2014中文版建筑制圖基礎培訓教程 [朱
- 2021-08-30電氣CAD實例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風暴2:Maya影像實拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術設計案例教程中文版AutoCAD 建筑設計案例
- 2021-08-29環境藝術制圖AutoCAD [徐幼光 編著] 2013年PDF下載
- 2021-08-29機械AutoCAD 項目教程 第3版 [繆希偉 主編] 2012年PDF




