副標題#e# 隨著計算機輔助設計制造技術的飛速發展,計算機仿真技術已成為工程技術人員極其重要的科研工具,文中利用計算機仿真技術精確地繪制出擺線輪的齒廓曲線,簡化了擺線輪齒廓的繪制過程,研究結果對提高擺線輪設計的速度和質量具有一定的實際意義。
COSMOSMotion是為廣大用戶提供的實現數字化功能樣機的優秀工具,它與當今主流的三維CAD軟件SolidWorks無縫集成,是全功能的運動仿真軟件,可以建立各種復雜運動機構的精確運動模型,并對運動機構進行完整的運動學和動力學仿真,得到機構中各零部件的運動數據,分析機構中零件的位移、速度、加速度、作用力與反作用力等,并以圖形、動畫、表格等多種形式輸出運算結果。大大簡化了機構的設計開發過程,縮短了開發周期,減少了開發費用,同時又提高了產品質量。總之,COSMOSMotion功能強大,求解可靠,仿真結果與實際情況十分吻合,完全能夠滿足用戶對運動仿真的各種需求。
作為普通減速機的更新換代產品,擺線針輪行星減速器與普通減速機相比,具有結構緊湊、傳動比大、傳動效率高、多齒嚙合、承載能力大等突出優點。擺線針輪行星減速器以其輸入輸出同軸、多齒嚙合的新穎結構,廣泛應用于礦山、冶金、工程機械及化工等行業的驅動裝置和減速裝置中瞄J。擺線針輪傳動采用圓柱面針齒與具有短幅外擺線等距曲線齒面的擺線輪相嚙合,擺線輪齒面形狀極為復雜,但對整個系統的承載能力與精度有極大影響,因此齒面的造型也極為重要。擺線輪的齒廓形狀因其特殊性給加工制造增加了難度,至今其齒廓還不能實現共軛切削加工,因此擺線輪的加工必須由齒廓外形圖來提供支持。利用COSMOSMotion的仿真功能可以很精確地將擺線輪的齒廓形狀表達出來,所以,探討利用COSMOSMotion進行擺線輪的三維設計方法具有實際的意義。
1 擺線輪齒廓曲線成形原理
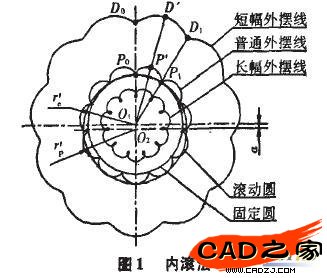
齒廓成形原理是繪制齒廓曲線的依據,形成外擺線的方法有內滾法和外滾法。內滾法如圖1所示,以半徑為ro的圓作固定圓,用半徑為rp的圓作為滾動圓套在固定圓外面,兩圓的半徑差就是其中心距,即a=rp-ro。當滾動圓繞固定圓滾過全周長2πrp時,與滾動圓同步滾動的任何一點均可形成一條完整的外擺線,這種形成外擺線的方法稱為內滾法。如果該點位于滾動圓的圓周上(如圖1中的Po點),由Po點形成的外擺線Po P P1。稱為普通外擺線。當該點位于滾動圓之外時(如圖1中的Do點),由現點形成的外擺線莉。稱為短幅外擺線,比值Kt=rp/O2D0稱為短幅系數。當該點位于滾動圓以內時,其軌跡為長幅外擺線。
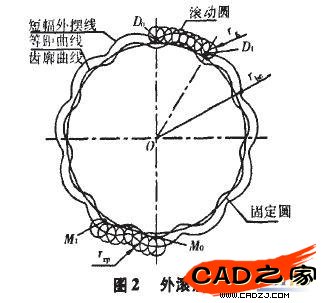
外滾法如圖2所示,在圖2中使半徑為rg的滾動圓G沿半徑為,rbc的固定圓J作純滾動,當滾動圓G沿固定圓.,滾過一周時,滾動圓內一點仇描繪出的軌跡DoD1是一條短幅外擺線,短幅系數為K1=ODo/rg。當滾動圓G沿固定圓J滾過2πrbc距離時,仇點描繪出的軌跡就是一條完整的擺線輪廓。
在擺線針輪行星齒輪傳動中,擺線輪是以短幅外擺線DOD1作為理論齒廓的,而固定針輪以Do點作為理論齒形。但是,實際針齒不可能做成一點,必須做成半徑為,。的圓柱形。因此,以擺線輪的理論齒廓上各點為圓心,以k為半徑作圓,這些圓的內包絡線眠麝。就是擺線輪的實際齒廓,又稱為短幅外擺線的等距曲線。而針輪的實際輪廓就是半徑為k的圓(如圖2所示),滾動圓中心所在圓的直徑為2rp,rp為滾動圓中心所在圓的半徑,也就是滾動圓G與固定圓J的中心距,即rP=rg+rbc。滿足以下3個條件時,采用外滾法形成的短幅外擺線與采用內滾法得到的短幅外擺線相同:
2 擺線輪齒廓曲線繪制方法
由于擺線輪齒廓曲面形狀的特殊性,有關其齒形輪廓設計方法的技術資料并不多。在擺線針輪傳動中,擺線輪齒廓的形狀誤差直接影響擺線針輪的傳動精度和傳動系統的運行壽命。擺線輪齒廓曲面的繪制關鍵在于擺線輪廓曲線的繪制,只要精確地繪制出擺線輪廓曲線,擺線輪齒廓曲面的三維造型即迎刃而解。
擺線輪的齒廓曲線是一種比較復雜的函數曲線,無法采用常規的造型方式。而利用COSMOSMotion的軌跡跟蹤功能,可以根據擺線輪齒廓曲線成形原理,通過簡單的運動仿真,即可精確地繪制出擺線輪廓曲線。下面通過具體實例詳細介紹具體繪制過程。
COSMOSMotion是為廣大用戶提供的實現數字化功能樣機的優秀工具,它與當今主流的三維CAD軟件SolidWorks無縫集成,是全功能的運動仿真軟件,可以建立各種復雜運動機構的精確運動模型,并對運動機構進行完整的運動學和動力學仿真,得到機構中各零部件的運動數據,分析機構中零件的位移、速度、加速度、作用力與反作用力等,并以圖形、動畫、表格等多種形式輸出運算結果。大大簡化了機構的設計開發過程,縮短了開發周期,減少了開發費用,同時又提高了產品質量。總之,COSMOSMotion功能強大,求解可靠,仿真結果與實際情況十分吻合,完全能夠滿足用戶對運動仿真的各種需求。
作為普通減速機的更新換代產品,擺線針輪行星減速器與普通減速機相比,具有結構緊湊、傳動比大、傳動效率高、多齒嚙合、承載能力大等突出優點。擺線針輪行星減速器以其輸入輸出同軸、多齒嚙合的新穎結構,廣泛應用于礦山、冶金、工程機械及化工等行業的驅動裝置和減速裝置中瞄J。擺線針輪傳動采用圓柱面針齒與具有短幅外擺線等距曲線齒面的擺線輪相嚙合,擺線輪齒面形狀極為復雜,但對整個系統的承載能力與精度有極大影響,因此齒面的造型也極為重要。擺線輪的齒廓形狀因其特殊性給加工制造增加了難度,至今其齒廓還不能實現共軛切削加工,因此擺線輪的加工必須由齒廓外形圖來提供支持。利用COSMOSMotion的仿真功能可以很精確地將擺線輪的齒廓形狀表達出來,所以,探討利用COSMOSMotion進行擺線輪的三維設計方法具有實際的意義。
1 擺線輪齒廓曲線成形原理
齒廓成形原理是繪制齒廓曲線的依據,形成外擺線的方法有內滾法和外滾法。內滾法如圖1所示,以半徑為ro的圓作固定圓,用半徑為rp的圓作為滾動圓套在固定圓外面,兩圓的半徑差就是其中心距,即a=rp-ro。當滾動圓繞固定圓滾過全周長2πrp時,與滾動圓同步滾動的任何一點均可形成一條完整的外擺線,這種形成外擺線的方法稱為內滾法。如果該點位于滾動圓的圓周上(如圖1中的Po點),由Po點形成的外擺線Po P P1。稱為普通外擺線。當該點位于滾動圓之外時(如圖1中的Do點),由現點形成的外擺線莉。稱為短幅外擺線,比值Kt=rp/O2D0稱為短幅系數。當該點位于滾動圓以內時,其軌跡為長幅外擺線。
外滾法如圖2所示,在圖2中使半徑為rg的滾動圓G沿半徑為,rbc的固定圓J作純滾動,當滾動圓G沿固定圓.,滾過一周時,滾動圓內一點仇描繪出的軌跡DoD1是一條短幅外擺線,短幅系數為K1=ODo/rg。當滾動圓G沿固定圓J滾過2πrbc距離時,仇點描繪出的軌跡就是一條完整的擺線輪廓。
在擺線針輪行星齒輪傳動中,擺線輪是以短幅外擺線DOD1作為理論齒廓的,而固定針輪以Do點作為理論齒形。但是,實際針齒不可能做成一點,必須做成半徑為,。的圓柱形。因此,以擺線輪的理論齒廓上各點為圓心,以k為半徑作圓,這些圓的內包絡線眠麝。就是擺線輪的實際齒廓,又稱為短幅外擺線的等距曲線。而針輪的實際輪廓就是半徑為k的圓(如圖2所示),滾動圓中心所在圓的直徑為2rp,rp為滾動圓中心所在圓的半徑,也就是滾動圓G與固定圓J的中心距,即rP=rg+rbc。滿足以下3個條件時,采用外滾法形成的短幅外擺線與采用內滾法得到的短幅外擺線相同:
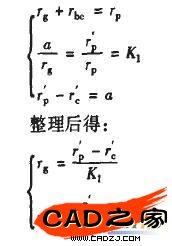
2 擺線輪齒廓曲線繪制方法
由于擺線輪齒廓曲面形狀的特殊性,有關其齒形輪廓設計方法的技術資料并不多。在擺線針輪傳動中,擺線輪齒廓的形狀誤差直接影響擺線針輪的傳動精度和傳動系統的運行壽命。擺線輪齒廓曲面的繪制關鍵在于擺線輪廓曲線的繪制,只要精確地繪制出擺線輪廓曲線,擺線輪齒廓曲面的三維造型即迎刃而解。
擺線輪的齒廓曲線是一種比較復雜的函數曲線,無法采用常規的造型方式。而利用COSMOSMotion的軌跡跟蹤功能,可以根據擺線輪齒廓曲線成形原理,通過簡單的運動仿真,即可精確地繪制出擺線輪廓曲線。下面通過具體實例詳細介紹具體繪制過程。

相關文章
- 2021-09-08BIM技術叢書Revit軟件應用系列Autodesk Revit族詳解 [
- 2021-09-08全國專業技術人員計算機應用能力考試用書 AutoCAD2004
- 2021-09-08EXCEL在工作中的應用 制表、數據處理及宏應用PDF下載
- 2021-08-30從零開始AutoCAD 2014中文版機械制圖基礎培訓教程 [李
- 2021-08-30從零開始AutoCAD 2014中文版建筑制圖基礎培訓教程 [朱
- 2021-08-30電氣CAD實例教程AutoCAD 2010中文版 [左昉 等編著] 20
- 2021-08-30電影風暴2:Maya影像實拍與三維合成攻略PDF下載
- 2021-08-30高等院校藝術設計案例教程中文版AutoCAD 建筑設計案例
- 2021-08-29環境藝術制圖AutoCAD [徐幼光 編著] 2013年PDF下載
- 2021-08-29機械AutoCAD 項目教程 第3版 [繆希偉 主編] 2012年PDF